Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Nhiệt lượng cần cung cấp để đun sôi nước là:
Qcó ích = m1.c.Δtº = 2.4200.(100 – 25) = 630000 (J)
Ta có:
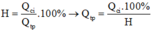
Nhiệt lượng do bếp điện tỏa ra là:
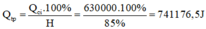
Vì U = Um = 220 nên bếp hoạt động với công suất P = Pm = 1000W
Ta có: Qtp = A = P.t
Thời gian đun sôi nước là: t = Qtp/P = 741176,5/1000 = 741 (s) = 12,35 phút
b) Nhiệt lượng do bếp tỏa ra để đun sôi 4 lít nước là:
Q1 = 2.Qtp = 2.741176,5 = 1482353 (J) (vì m2 = 4kg = 2m1)
Nhiệt lượng do bếp điện tỏa ra trong 30 ngày là:
Q2 = 1482353.30 = 44470590 (J)
Điện năng tiêu thụ trong 1 tháng là:
A = Q2 = 44470590 J = 12,35kW.h (vì 1kW.h = 3600000J)
Tiền điện phải trả là: Tiền = A.700 = 12,35.700 = 8645 đồng
c) Do gập đôi dây điện trở nên: tiết diện dây tăng 2 lần ⇒ điện trở giảm 2 lần
và chiều dài dây giảm 2 lần ⇒ điện trở giảm 2 lần. Vậy R giảm 4 lần
Dựa vào công thức P = U2/R nên khi R giảm 4 lần thì P tăng 4 lần, khi đó:
P’ = 4.1000 = 4000 (W)
Thời gian đun sôi nước là: t’ = Qtp/P = 741176,5/4000 = 185 (s) = 3,08 phút

Công suất của ấm điện là:
\(P=\dfrac{U^2}{R}=\dfrac{220^2}{30,25}=1600\left(W\right)\)
Nhiệt lượng nước tỏa ra:
\(Q_{tỏa}=A=P.t=1600.7.60=672000\left(J\right)\)
Nhiệt lượng nước thu vào:
\(H=\dfrac{Q_{thu}}{Q_{tỏa}}\Rightarrow Q_{thu}=H.Q_{tỏa}=80\%.672000=537600\left(J\right)\)
\(mc\Delta t=Q_{thu}\Rightarrow m=\dfrac{Q_{thu}}{c\Delta t}=\dfrac{537600}{4200.\left(100-20\right)}=1,6\left(kg\right)\)
Điện năng ấm tiêu thụ trong 30 ngày:
\(A=P.t=1600.30.45.60=129600000\left(J\right)=36\left(kWh\right)\)
Tiền điện phải trả: \(36.1600=57600\left(đ\right)\)

Điện trở ấm:
\(R_â=\dfrac{U_â^2}{P_â}=\dfrac{220^2}{1000}=48,4\Omega\)
Điện năng ấm tiêu thụ trong 14 phút:
\(A=UIt=220\cdot\dfrac{220}{48,4}\cdot14\cdot60=840000J\)
Nhiệt lượng cần thiết để đun sôi 2l nước:
\(Q=mc\Delta t=2\cdot4200\cdot\left(100-20\right)=672000J\)
Hiệu suất ấm:
\(H=\dfrac{Q}{A}=\dfrac{672000}{840000}\cdot100\%=80\%\)
a. R = U2/P = 2202/1000 = 48.4 ohm
b. Qtỏa = P*t = 1000*14*60 = 840000 J
Qthu = m*c*△t = 2*4200*80 = 672000 J
=> H% = Qthu / Qtỏa *100% = 672000 / 840000 *100% = 80%

Điện trở của ấm điện trên là:
\(P=\dfrac{U^2}{R}\Rightarrow R=\dfrac{U^2}{P}=\dfrac{220^2}{1000}=48,4\left(\Omega\right)\)
Nhiệt lượng bếp tỏa ra trong 12ph:
\(Q_{tỏa}=A=P.t=1000.12.60=720000\left(J\right)\)
Nhiệt lượng bếp thu vào:
\(Q_{thu}=mc\Delta t=2.4200.\left(100-20\right)=672000\left(J\right)\)
Hiệu suất của bếp:
\(H=\dfrac{Q_{thu}}{Q_{tỏa}}.100\%=\dfrac{672000}{720000}.100\%\approx93,3\%\)

`*` Tóm tắt:
`mathcalP = 880W`
\(S=0,2mm^2=0,2\cdot10^{-6}m^2\\ \rho=4,4\cdot10^{-7}\Omega\cdot m\\ U=220V\\ m=2,5l=2,5kg\\ t_0=100^oC\\ t_1=28^oC\\ H=90\%\\ c=4200J/kg\cdot K\\ -------------\\ a)l=?m\\ b)t=?s\)
_
`*` Giải:
`a)` Điện trở của bếp điện:
`R = (U^2)/(mathcalP) = (220^2)/880 = 55\Omega`
Chiều dài dây điện trở bếp điện:
\(R=\dfrac{\rho\cdot l}{S}\Rightarrow l=\dfrac{R\cdot S}{\rho}=\dfrac{55\cdot0,2\cdot10^{-6}}{4,4\cdot10^{-7}}=25m\)
`b)` Ta có: \(Q=m\cdot c\cdot\left(t_0-t_1\right)\)
Và: nhiệt lượng do vật tỏa ra bằng công của dòng điện `Q=A`
Thời gian đun sôi nước:
`A=Q=mathcalP * t => t = Q/(mathcalP) =`\(\dfrac{2,5\cdot4200\cdot\left(100-28\right)}{880}\approx859,1s.\)

a) Nhiệt lượng cần cung cấp để đun sôi lượng nước trên là:
Q1 = c.m.(T – T0) = 4200.2.(100 - 20) = 672000 (J)
b) Hiệu suất của bếp: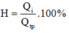
Nhiệt lượng mà ấm điện đã tỏa ra khi đó là:
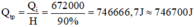
c) Từ công thức: Qtp = A = P.t
→ Thời gian đun sôi lượng nước:
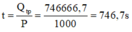
a) Nhiệt lượng cần cung cấp để đun sôi lượng nước trên là:
Q1 = c.m.(T – T0) = 4200.2.(100 - 20) = 672000 (J)
b) Hiệu suất của bếp: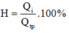

Nhiệt lượng cần cung cấp để đun sôi 1,5 lít nước là:
Q = 420000.1,5 = 630000 J
Theo công thức tính nhiệt lượng tỏa ra của ấm ta có:
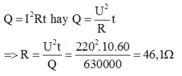
→ Đáp án C
Nhiệt lượng cần cung cấp để đun sôi nước:
\(Q_i=mc\left(t_2-t_1\right)=0,12\cdot4200\cdot\left(100-10\right)=45360J\)
Hiệu suất của ấm là 60% nên \(H=\dfrac{Q_i}{A}=60\%\)
\(\Rightarrow\) Điện năng ấm tiêu thụ trong 10 phút là:
\(A=\dfrac{Q_i}{H}=\dfrac{45360}{60\%}=75600J\)
Mặt khác: \(A=UIt=\dfrac{U^2}{R}\cdot t\)
\(\Rightarrow75600=\dfrac{100^2}{R}\cdot10\cdot60\Rightarrow R=\dfrac{5000}{63}\Omega\)
Lại có: \(R=\rho\cdot\dfrac{l}{S}\Rightarrow\dfrac{5000}{63}=4\cdot10^{-7}\cdot\dfrac{l}{\pi\cdot\left(\dfrac{0,2\cdot10^{-3}}{2}\right)^2}\)
\(\Rightarrow l=\dfrac{125\pi}{63}\)
Độ dài một vòng quấn: \(C=2\pi R=\pi\cdot D=1,5\pi\left(cm\right)=0,015\pi\left(m\right)\)
Số vòng quấn: \(N=\dfrac{l}{C}=\dfrac{\dfrac{125\pi}{63}}{0,015\pi}=\dfrac{25000}{189}\approx133\left(vòng\right)\)