Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
+) Chọn 3 tiết mục bất kì có C 9 3 = 84 (cách).
+) Chọn 1 tiết mục của khối 10 có 3 cách. Chọn tiếp 1 tiết mục của khối 11 không trùng với nội dung đã chọn của khối 11 có 2 cách. Chọn tiếp 1 tiết mục của khối 12 không trùng với nội dung đã chọn của khối 10 và khối 11 có 1 cách. Do đó cá 6 cách chọn các tiết mục thoản mãn yêu cầu đề bài.
Vậy xác suất cần tính là 6 84 = 1 14
Chọn A.
Chọn ngẫu nhiên 5 học sinh trong số 48 học sinh có:
- Gọi A là biến cố "chọn 5 học sinh trong đó có ít nhất một học sinh nữ" thì 
là biến cố "chọn 5 học sinh mà trong đó không có học sinh nữ".
- Ta có số kết quả thuận lợi cho 
là:
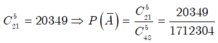
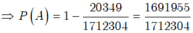
Số cách chia 14 tiết mục thành 2 nhóm là: \(n(\Omega )= C_{14}^{7}.C_{7}^{7} \)
Gọi A là biến cố 2 tiết mục của lớp 12a1 được biểu diễn cùng một nhóm.
Số cách chọn 1 trong 2 nhóm để xếp 2 tiết mục của lớp 12a1 vào là: \( C_{2}^{1}\)
Số cách xếp 12 tiết mục còn lại là: \(C_{12}^{5}.C_{7}^{7}\)
Ta có \(n(A)= C_{2}^{1}.C_{12}^{5}.C_{7}^{7} \)
Xác suất xảy ra A là: \(P(A)= \frac{n(A)}{n(\Omega )} = \frac{C_{2}^{1}.C_{12}^{5}.C_{7}^{7}}{C_{14}^{7}.C_{7}^{7} } = \frac{6}{13} \)
Chọn D
Vì mỗi học sinh lớp 12A được đăng kí 1 hoặc 2 tiết mục trong số 3 tiết mục văn nghệ nên số cách lựa chọn tiết mục văn nghệ của mỗi học sinh là: C 3 1 + C 3 2 = 6.
Lớp 12A có 44 học sinh đều tham gia văn nghệ nên số cách để lớp lựa chọn là: 6 44 .
Xét 2 biến cố:
D: “Bạn Hương được chọn song ca” => P(D) = 0,9
E: “Bạn Dũng được chọn song ca” => P(E) = 0,7
a) Do \(A = D \cap E \Rightarrow P(A) = P(D).P(E) = 0,7.0,9 = 0,63\)
b) Ta thấy \(B = E \cup D \Rightarrow P(B) = P(E \cup D) = P(E) + P(D) - P(E \cap D) = 0,7 + 0,9 - 0,63 = 0,97\)
c) Xét biến cố đối \(\overline D \) của biến cố D. Ta thấy \(P\left( {\overline D } \right) = 1 - P(D) = 1 - 0,9 = 0,1\)
Vì \(C = E \cap \overline D \Rightarrow P(C) = P(E).P\left( {\overline D } \right) = 0,1.0,7 = 0,07\)
chọn 5 đội trong 12 đội có \(C^5_{12}=792\) cách
=> \(n\left(\Omega\right)=792\)
Gọi A:" 5 đội được chọn có ít nhất 1 đội cờ đỏ khối 10 và ít nhất 1 đội cờ đỏ khối 11 "
+) 1 đội K10 +4 đội K11 => có \(C^1_5.C^4_7=175\) cách
+) 2 đội K10 +3 đội K11 => có \(C^2_5.C^3_7=350\)cách
+) 3 đội k10 + 2 đội k11 => có \(C^3_5.C^2_7=210\) cách
+) 4 độ k10 + 1 đội k11 => có \(C^4_5.C^1_7=35\)cách
=> n(A) = 175+350+210+35 = 770
=> P(A) = 770/792=35/36
a) \(n\left(\Omega\right)=C^3_{10}\)
Chọn 2 tiết mục hát : \(C^2_5\)
Chọn 1 tiết mục còn lại : 5
P = \(\frac{C^2_5\cdot5}{C^3_{10}}=\frac{5}{12}\)
b) P = \(\frac{5\cdot3\cdot2}{C^3_{10}}=\frac{1}{4}\)
Đáp án A
Chọn 3 tiết mục bất kỳ có: Ω = C 9 3 = 84 cách.
Gọi A là biến cố: “ba tiết mục được chọn có đủ cả ba khối và đủ cả ba nội dung”.
Khối 10 chọn 1 tiết mục có 3 cách
khối 11 chọn 1 tiết mục khác khối 10 có 2 cách
tương tự khối 12 có 1 cách
Ta có: Ω A = 3 . 2 . 1 = 6 cách
Vậy P = 6 84 = 1 14