Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi số cuối cùng nghĩa đọc ra là X
theo bài ra ta có
[ ( x+5).2-10]+66/6 = X
⇔[(x+5).2–10].3+66 / 6=X
⇔[2x+10–10].3+66 / 6=X
⇔ 6x+66 / 6=X
⇔x + 11 = X
⇔x = X – 11
Vậy Trung chỉ cần làm phép trừ số cuối cùng của Nghĩa đọc lên với 11 thì được số của Nghĩa đã nghĩ ra.

Bí quyết của Trung lấy kết quả cuối cùng của Nghĩa đem trừ 11 thì được số của Nghĩa nghĩ ra lúc đầu.
Thật vậy:
- Gọi x là số mà Nghĩa nghĩ. Theo đề bài số cuối cùng của Nghĩa đọc ra là:
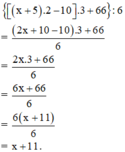
Vậy Trung chỉ cần làm phép trừ số cuối cùng của Nghĩa đọc lên cho số 11 thì được số của Nghĩa đã nghĩ ra.

Giả sử số lúc đầu là x.
Theo đề bài, ta có phương trình:
\(\left\{\left[\left(x+5\right).2-10\right].3+66\right\}:6\)
\(=\left[\left(2x+10-10\right).3+66\right]:6=\left(2x.3+66\right):6=\left(6x+66\right):6=6\left(x+11\right):6=x+11\)
Vậy chỉ cần lấy kết quả sau cùng trừ đi 11 ta được số lúc đầu

Bí quyết của Trung lấy kết quả cuối cùng của Nghĩa đem trừ 11 thì được số của Nghĩa nghĩ ra lúc đầu.
Thật vậy:
- Gọi x là số mà Nghĩa nghĩ. Theo đề bài số cuối cùng của Nghĩa đọc ra là:
Vậy Trung chỉ cần làm phép trừ số cuối cùng của Nghĩa đọc lên cho số 11 thì được số của Nghĩa đã nghĩ ra.


Gọi số cần tìm là \(x\)
Vì bình nghĩ 1 số nếu lấy số đó nhân 5 cộng với 10 được bao nhiêu chia cho 5 tiếp tục lấy thương trừ 15 rồi cộng thêm 10 được 2 nên ta có phương trình:
\(\frac{5x+10}{5}-15+10=2\)
\(\Rightarrow\frac{5x+10}{5}-\frac{5.15}{5}+\frac{5.10}{5}=\frac{2.5}{5}\)
\(\Rightarrow5x+10-75+50=10\)
\(\Rightarrow5x-15=10\)
\(\Rightarrow5x=25\Rightarrow x=5\)
Vậy số cần tìm là \(5\)

Ta có :
\(\left(2x-10\right)\cdot3+40=100\)
=> \(6x-30+40-100=0\)
=> \(x=15\)
Gọi số cần tìm là a
Theo bài ra ta có :
3( 2a - 10 ) + 40 = 100
3( 2a - 10 ) = 60
2x - 10 = 20
2x = 30
x = 15
Vậy x = 15 thỏa mãn đề bài
