Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Tự vẽ nhé!
b)Vì là TKHT nên:
-Khoảng cách của ảnh là:
\(\frac{1}{f}=\frac{1}{d}+\frac{1}{d^'}\Leftrightarrow\frac{1}{12}=\frac{1}{36}+\frac{1}{d^'}\)
\(\Leftrightarrow\frac{1}{d^'}=\frac{1}{12}-\frac{1}{36}=\frac{1}{18}\Leftrightarrow d^'=18\left(cm\right)\)
-Độ cao của ảnh là:
\(\frac{h}{h^'}=\frac{d}{d^'}\)
\(\Leftrightarrow\frac{1}{h'}=\frac{12}{18}\Leftrightarrow h'=18.1:12=1,5\left(cm\right)\)
xétΔOAB và ΔOA'B'
ABA′B′=OAOA′ABA′B′=OAOA′⇒ABA′B′=8OA′(1)ABA′B′=8OA′(1)
xétΔOFI và ΔF'A'B'
OIA′B′=12OF′+OA′OIA′B′=12OF′+OA′(2)
từ (1) và (2)⇒8OA′=1212+OA′8OA′=1212+OA′
⇔8.(12+OA')=12.OA'
⇔96+8.OA'=12.OA'
⇔8.OA'-12.OA'=96
⇔-4.OA'=96
⇔OA'=-24 cm
thay OA'=-24 vào (1)
1A′B′=8−241A′B′=8−24⇒A'B'=−13−13 cm

a) vì là TKHT mà theo đề thì ta có d (tức là OA) < f ,=> ảnh ảo, cùng chiều và lớn hơn vật
b)Xét tam giác OAB đồng dạng vs ta, giác OA'B'
=> h/h' = d/d' (AB/A'B'=OA/OA')..........(1)
xét tam giac F'OI đồng dạng vs tgiac F'A'B'
=> h/h' = f/(f+d') (( OI/A'B' = FO/(FO+FA')))..........(2)
từ 1 và 2 => d/d' =f/(f+d')
chia 2 vế cho dd'f => 1/d =1/f + 1/d'
theo đề có d và f => d'=12
thế d'=12, d=6, h=1 vào (1)
=>h'=2
F' A O A' B' I

a. Thấu kính này là TLHT vì ảnh ngược chiều vs vật...cho ảnh thật,,...
b. hình tự vẽ...
f= OF = OF'= 4.8 cm

Khoảng cách ảnh AB tới thấu kính \(d_2\):
\(\dfrac{1}{f_2}=\dfrac{1}{d_2}+\dfrac{1}{d_2'}\Rightarrow d_2'=\dfrac{d_2\cdot f_2}{d_2-f_2}=\dfrac{9d_2}{d_2-9}\left(cm\right)\)
Di chuyển thấu kính lại gần màn ảnh 24 cm:
\(\Rightarrow d_2"=\dfrac{\left(d_2+24\right)\cdot f_2}{d_2+24-f_2}=\dfrac{9\left(d_2+24\right)}{d_2+15}\left(cm\right)\)
Khoảng cách giữa ảnh AB và O1 là:
\(d_2+\dfrac{9d_2}{d_2-9}=d_2+24+\dfrac{9\left(d_2+24\right)}{d_2+15}\)
\(\Rightarrow d_2^2+6d_2-216=0\Rightarrow\left[{}\begin{matrix}d_2=12cm\\d_2=-18cm\left(loại\right)\end{matrix}\right.\)
Ảnh AB cách thấu kính O1:
\(d_1'=60-12-36=12cm\)
Tiêu cự thấu kính O1:
\(\dfrac{1}{f_1}=\dfrac{1}{d_1}+\dfrac{1}{d_1'}=\dfrac{1}{12}+\dfrac{1}{12}=\dfrac{1}{6}\)
\(\Rightarrow f_1=6cm\)
Tịnh tiến AB trước thấu kính O để ảnh độ cao không phụ thuộc vào vị trí của vật.
Xảy ra\(\Leftrightarrow\)Tiêu điểm hai thấu kính trùng nhau.
\(\Leftrightarrow O_1O_2=f_1+f_2=6+9=15cm\)

MÌNH THAM KHẢO NHÉ
a) Xét △ABO và △A′B′O có:
ABOˆ=A′B′Oˆ=900
BOAˆ=B′OA′ˆ (hai góc đối đỉnh)
⇒ Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
⇒ \(\frac{A'B'}{AB}=\frac{B'O}{BO}\)
⇒ Độ phóng đại ảnh \(k=\frac{A'B'}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự: Hai tam giác A'B'F' và IOF' là hai tam giác đồng dạng
⇒\(\text{ }\frac{B'F'}{OF'}=\frac{A'B'}{IO}=\frac{d'}{d}\)
Áp dụng tính chất của tỉ lệ thức: \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)
⇒\(\frac{1}{f}=\frac{1}{d}=\frac{1}{f'}\)
CÓ MẤY CÁI KÍ HIỆU GÓC, MÌNH KHÔNG BIẾT VIẾT, BẠN THÔNG CẢM
a) Xét \(\Delta ABO\) và \(\Delta A'B'O'\)
\(ABO=A'B'O=90^0\)
\(BOA=B'O'A\)( hai góc đối đỉnh )
\(\Rightarrow\)Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
\(\Rightarrow\frac{A'B}{AB}=\frac{B'O}{BO}\)
\(\Rightarrow\)Độ phóng đại ảnh : \(k=\frac{A'B}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự : Hai tam giác A'B'F và IOF' là hai tam giác đồng dạng
\(\Rightarrow\frac{B'F'}{OF}=\frac{A'B}{TO}=\frac{d'}{d}\)
Dựa vào tính chất của tỉ lệ thức : \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)

a, Vẽ ảnh A'B'
A B A' B' F F' O I
b,
Gọi khoảng cách từ AB đến thấu kính là d, từ A'B' đến thấu kính là d'
Xét \(\Delta ABO \sim \Delta A'B'O\)
\(\Rightarrow \dfrac{AB}{A'B'}=\dfrac{BO}{B'O}=\dfrac{10}{d'}\)(1)
Xét \(\Delta IOF \sim \Delta A'B'F\)
\(\Rightarrow \dfrac{IO}{A'B'}= \dfrac{OF}{B'F}\)
Ta có: \(IO=AB\)
\(\Rightarrow \dfrac{AB}{A'B'}= \dfrac{14}{d'+14}\)(2)
Từ (1) và (2) \(\Rightarrow\dfrac{10}{d'}=\dfrac{14}{d'+14}\)
\(\Rightarrow d'=35cm\)
Vậy ảnh cách thấu kính 35 cm
Thế vào (1) ta được: \(\Rightarrow \dfrac{AB}{A'B'}=\dfrac{10}{35}\Rightarrow A'B' = \dfrac{35.2}{10}=7(cm)\)
Vậy ảnh cao 7cm.

Tóm tắt:
TKHT có f = 12 cm
Vật sáng AB cao 1cm đặt vuông góc với trục chính tại A.
Khoảng cách vật – tk: d= 8 cm.
a. Vẽ ảnh A’B’ của vật AB
b. Nêu đặc điểm của ảnh.
c. Tính khoảng cách từ ảnh đến thấu kính và chiều cao của ảnh.
Giải:
a. Vẽ hình minh họa sự tạo ảnh
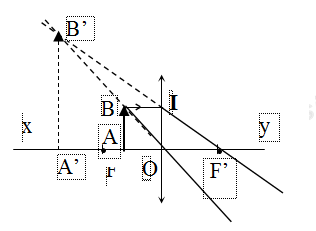
b. Vì vật nằm trong khoảng tiêu cự của thấu kính (d
c. Xét tam giác OAB và tam giác OA’B’ có: góc O chung; góc A = góc A’ = 900.
Nên tam giác OAB đồng dạng với tam giác OA’B’. Ta có các tỉ số đồng dạng:
ABA′B′=AOA′O⇔hh′=dd′ABA′B′=AOA′O⇔hh′=dd′
Xét tam giác OIF’ và tam giác F’A’B’
Có:
IF′O=ˆB′F′A′IF′O^=B′F′A′^
; ˆO=ˆA′=900O^=A′^=900
Nên tam giác OIF’ ~ tam giác F’A’B’ . Ta có tỉ số đồng dạng:
OIA′B′=OF′F′A′⇔ABA′B′=OF′OA′+OF′⇔dd′=fd′+fOIA′B′=OF′F′A′⇔ABA′B′=OF′OA′+OF′⇔dd′=fd′+f
Thay số từ đề bài ta có:
8d′=12d′+12⇔8d′+96=12d′⇔4d′=96⇔d′=24cm⇔hh′=dd′⇔h′=h.d′d=1.248=3cm