Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

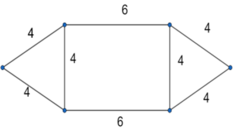
Hình lục giác đã cho là hợp của 2 tam giác đều có độ dài cạnh là 4 và 1 hình chữ nhật với độ dài 2 cạnh là 4 và 6.
Diện tích mỗi tam giác đều là 1 2 .4.4. sin 60 ° = 4 3 .
Diện tích hình chữ nhật là 24.
Diện tích của hình lục giác là: 4 3 + 4 3 + 24 = 8 3 + 24
ĐÁP ÁN D

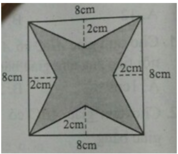
Diện tích phần được tô màu bằng hiệu diện tích của hình vuông cạnh 8cm và 4 tam giác bằng nhau có 1 cạnh bằng 8 và đường cao ứng với cạnh đó bằng 2 cm.
Diện tích của 1 tam giác là: S = 1 2 .2.8 = 8
Diện tích hình vuông là: S ’ = 8 2 = 64
Diện tích phần tô đậm là: 64 – 4.8 = 32.
ĐÁP ÁN B

\(AC=\sqrt{AB^2+BC^2-2AB.BC.cosB}=\sqrt{9^2+12^2-2.9.12.cos60^0}=3\sqrt{13}\)

\(S=\dfrac{1}{2}\left|\left(x_B-x_A\right)\left(y_C-y_A\right)-\left(x_C-x_A\right)\left(y_B-y_A\right)\right|\)
\(=\dfrac{1}{2}\left|\left(2-1\right)\left(-8+5\right)-\left(13-1\right)\left(1+5\right)\right|=\dfrac{75}{2}\)

Tham khảo:
a) Áp dụng hệ quả của định lí cosin, ta có:
\(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \left\{ \begin{array}{l}\cos A = \frac{{{{10}^2} + {{13}^2} - {8^2}}}{{2.10.13}} = \frac{{41}}{{52}} > 0;\\\cos B = \frac{{{8^2} + {{13}^2} - {{10}^2}}}{{2.8.13}} = \frac{{133}}{{208}} > 0\\\cos C = \frac{{{8^2} + {{10}^2} - {{13}^2}}}{{2.8.10}} = - \frac{1}{{32}} < 0\end{array} \right.\end{array}\)
\( \Rightarrow \widehat C \approx 91,{79^ \circ } > {90^ \circ }\), tam giác ABC có góc C tù.
b)
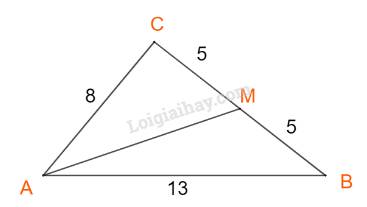
+) Áp dụng định lí cosin trong tam giác ACM, ta có:
\(\begin{array}{l}A{M^2} = A{C^2} + C{M^2} - 2.AC.CM.\cos C\\ \Leftrightarrow A{M^2} = {8^2} + {5^2} - 2.8.5.\left( { - \frac{1}{{32}}} \right) = 91,5\\ \Rightarrow AM \approx 9,57\end{array}\)
+) Ta có: \(p = \frac{{8 + 10 + 13}}{2} = 15,5\).
Áp dụng công thức heron, ta có: \(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {15,5.(15,5 - 8).(15,5 - 10).(15,5 - 13)} \approx 40\)
+) Áp dụng định lí sin, ta có:
\(\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{{13}}{{2.\sin 91,{{79}^ \circ }}} \approx 6,5\)
c)

Ta có: \(\widehat {BCD} = {180^ \circ } - 91,{79^ \circ } = 88,{21^ \circ }\); \(CD = AC = 8\)
Áp dụng định lí cosin trong tam giác BCD, ta có:
\(\begin{array}{l}B{D^2} = C{D^2} + C{B^2} - 2.CD.CB.\cos \widehat {BCD}\\ \Leftrightarrow B{D^2} = {8^2} + {10^2} - 2.8.10.\cos 88,{21^ \circ } \approx 159\\ \Rightarrow BD \approx 12,6\end{array}\)

\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=-\dfrac{1}{32}\)
\(\Rightarrow A\approx92^0\)
\(p=\dfrac{AB+AC+BC}{2}=\dfrac{31}{2}\)
\(S_{ABC}=\sqrt{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}\simeq40\)
\(r=\dfrac{S}{p}=\dfrac{80}{31}\)
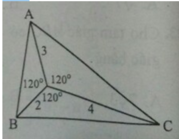



S = 1 2 .2.3. sin 120 ° + 1 2 .3.4. sin 120 ° + 1 2 .4.2. sin 120 ° = 13 3 2
ĐÁP ÁN B