Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Cường độ dòng điện hiệu dụng I = U/Z
Đoạn mạch gồm RLC mắc nối tiếp: I = U R 2 + Z L − Z C 2 ( 1 )
Khi nối tắt tụ: I = U R 2 + Z L 2
Từ (1) và (2) ⇒ U R 2 + Z L − Z C 2 = U R 2 + Z L 2 ⇒ Z L − Z C = Z L ( l o a i ) Z L − Z C = − Z L
⇒ 2 Z L = Z C ⇔ 2 ω L = 1 ω C ⇒ ω 2 L C = 0,5

Đáp án B
Do u và i dao động vuông pha => tại mọi thời điểm ta có:


Đáp án A
Phương pháp: Sử dụng hệ thức của định luật Ôm và công thức tính công suất tiêu thụ
Cách giải:
Giả sử cuộn dây thuần cảm:
Ta có, khi R = R 2 công suất tiêu thụ trên biến trở cực đại
Khi đó ta có: R 2 = | Z L - Z C | = 40 - 25 = 15 W
Mặt khác: P R 2 = U 2 2 R 2 = 120 2 2.15 = 480 ≠ 160
⇒ điều giả sử ban đầu là sai
⇒ Cuộn dây không thuần cảm có điện trở r
- Ta có:
+ Ban đầu khi mắc vào hai đầu A, M một ắc quy có suất điện động E = 12V, điện trở trong r 1 = 4 W thì I 1 = 0 , 1875
Theo định luật Ôm, ta có: I 1 = E R b + r = E R 1 + r + r 1 → R 1 + r 1 + r = E I 1 = 64 → R 1 + r = 60 Ω ( 1 )
+ Khi mắc vào A,B một hiệu điện thế u = 120 2 cos 100 π t , R = R 2 thì công suất tiêu thụ trên biến trở cực đại và bằng 160W
Ta có:
Công suất trên biến trở R đạt cực đại khi R 2 2 = r 2 + Z L − Z C 2 ( 2 )
Mặt khác, ta có:
Công suất trên R 2 : P = U 2 ( R 2 + r ) 2 + Z L − Z C 2 R 2 = 160 W → R 2 ( R 2 + r ) 2 + Z L − Z C 2 = 160 120 2 = 1 90
90 R 2 = 2 R 2 2 + 2 r R → R 2 + r = 45
Kết hợp với (2) ta được: R 2 2 = ( 45 − R 2 ) 2 + 15 2 → R 2 = 25 Ω , r = 20 Ω
Với r = 20W thay vào (1) ⇒ R 1 = 60 - 20 = 40 Ω
→ R 1 R 2 = 40 25 = 1,6

Đáp án B
Phương pháp: Cường độ dòng điện hiệu dụng I = U / Z C
Cách giải:
- Khi mắc vào mạng điện 110V - 60Hz thì I 1 = 1 , 5 A
Ta có: I 1 = U 1 Z C 1 → Z C 1 = U 1 I 1 = 110 1,5 = 220 3 Ω
Mặt hác, ta có: Z C 1 = 1 ω 1 C → C = 1 Z C 1 ω 1 = 1 Z C 1 2 π f 1 = 1 220 3 2 π .60 = 1 8800 π
- Khi mắc vào mạng điện 220 - 50Hz
Z C 2 = 1 ω 2 C = 1 2 π f 2 C = 1 2 π .50. 1 8800 π = 88 Ω ⇒ I 2 = U 2 Z C 2 = 220 88 = 2,5 A

Đáp án D
Phương pháp: Sử dụng công thức tính độ lệch pha giữa u và i
Cách giải:
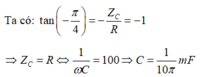
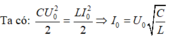
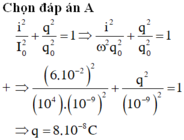
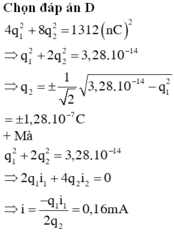
Đáp án D
Phương pháp: Sử dụng hệ thức vuông pha của i và u
Cách giải:
Ta có: i 2 I 0 2 + u 2 U 0 2 = 1 ⇒ 0,16 2 I 0 2 + 8 2 U 0 2 = 1 0,2 2 I 0 2 + 4 2 U 0 2 = 1 ⇒ I 0 2 = 28 625 U 0 2 = 448 3
Lại có: L I 0 2 2 = C U 0 2 2 ⇒ C = L I 0 2 U 0 2 = 50.10 − 3 . 28 625 448 3 = 1,5.10 − 5 F = 15 μ F