Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì ∆ ABC đồng dạng với ∆ AMN nên:
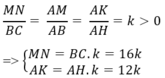
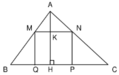
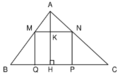
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
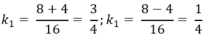
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
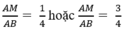

Vì ∆ ABC đồng dạng với ∆ AMN nên:
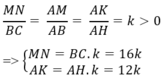
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
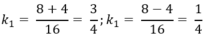
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
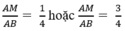

1: \(AB=\sqrt{AH^2+HB^2}=\sqrt{20+16}=6\left(cm\right)\)
\(AC=\sqrt{AH^2+HC^2}=3\sqrt{5}\)
Vì AB^2+AC^2=BC^2
nên ΔABC vuông tại A
=>tâm là trung điểm của BC
Bán kính là BC/2=4,5cm
2:Gọi Llà trung điểm của HK
Xét (L) có
HK là đường kính
nên H thuộc (L)

a: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
HB/HA=HA/HC
=>ΔHBA đồng dạng với ΔHAC
=>góc HBA=góc HAC
=>góc HBA+góc HCA=90 độ
=>góc BAC=90 độ
=>ΔBAC nội tiếp đường tròn đường kính BC
Tâm là trung điểm của BC
Bán kính là R=BC/2=4,5
b: Gọi giao của HI với AB là M, HK với AC là N
H đối xứng I qua AB
=>HI vuông góc AB tại M
H đối xứng K qua AC
=>HK vuông góc AC tại N
Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
=>góc MHN=90 độ
=>góc IHK=90 độ