Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

T = 0,63s ⇒ ω = 10
Tại t = 0 vật ở biên dương nên phương trình dao động của vật là
x = 10cos10t (cm)

Chọn đáp án C
T = 2 π m k = 0 , 2 s
Vì hệ có thêm lực điện nên VTCB của vật bị dịch về phí theo chiều lò xo dãn 1 khoảng là:
Δ x = F k = E . q k = 10 5 .2.10 − 5 100 ⇒ ∆ x = 0 , 02 m = 2 c m
Suy ra tại VTCB lò xo giãn 2 cm.
Ban đầu kéo lò xo dãn 6 cm rồi thả nhẹ
→ A = 6 – 2 = 4 cm và ban đầu vật đang ở biên dương.
Vị trí lò xo không biến dạng là:
x = − 2 c m = − A 2 c m
Suy ra khoảng thời gian để vật đi qua vị trí lò xo không biến dạng lần thứ 2013 là:
Δ t = T 3 + 2013 − 1 2 . T = 201 , 3 s .

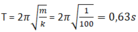
Tại t = 0 vật được kéo ra khỏi vị trí cân bằng cho lò xo dãn ra 10 cm rồi thả ra không vận tốc đầu nên biên độ A = 10 cm

Con lắc lò xo nằm ngang → Khi lò xo dãn 2 cm, li độ vật có độ lớn x = 2 c m
→ v = ω A 2 - x 2 = 20 π 3 cm / s . Chọn C.

Hướng dẫn:
+ Độ biến dạng của lò xo tại các vị trí cân bằng tạm x 0 = μ m g k = 0 , 05.1.10 100 = 5 m m
Vật bị nén nhiều nhất khi vật chuyển động hết nửa chu kì đầu tiên
→ Trong nửa chu kì đầu vật đi được quãng đường S = 2 X 0 − x 0 = 2 10.10 − 2 − 5.10 − 3 = 0 , 19 m
→ Lực ma sát đã sinh công A = F m s S = μ m g S = 0 , 095 J .
Đáp án C

Chọn C
+ ω = 2π : T = 20 rad/s.
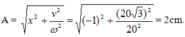
+ t = 0: x = 2cosφ = -1 => 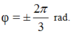
v = -40 sinφ > 0 => sinφ < 0 => ![]()
Vậy: x = 2 cos(20t - 2π/3) = 2 sin(20t - π/6) cm.
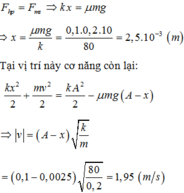
\(\omega=\sqrt{\dfrac{k}{m}}=10\left(rad\text{/}s\right)\)
\(\overrightarrow{F_đ}=Q\overrightarrow{E}\)
Vị trí cân bằng mới, lò xo đã dãn được 1 đoạn \(\Delta l=\dfrac{QE}{k}=2\left(cm\right)\)
\(t=0\left\{{}\begin{matrix}x=2cm\\v=20\sqrt{3}cm\text{/}s\end{matrix}\right.\Rightarrow A=\sqrt{x^2+\dfrac{v^2}{\omega^2}}=4\left(cm\right)\)
\(\left\{{}\begin{matrix}\cos\varphi=\dfrac{1}{2}\\\sin\varphi< 0\end{matrix}\right.\Rightarrow\varphi=-\dfrac{\pi}{3}\)
Vậy phương trình dao động của vật là: \(x=4\cos\left(10t-\dfrac{\pi}{3}\right)cm\)