Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

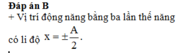

Đáp án C
Cơ năng của con lắc lò xo được xác định bằng biểu thức E = 1 2 k A 2

Chọn A
+ Động năng bằng thế năng ở vị trí x = ±A√2/2 = ±√2 cm và v = ωA/√2 = 6π cm.
+ Khi mo rơi và dính vào m, theo định luật bảo toàn động lượng (chú ý là vật m0 rơi thẳng đứng nên động lượng của nó theo phương ngang = 0): (m+mo)v’ = mv => v’ = 4π cm/s.
+ Hệ (m + mo) có ω’ = 2π√3 rad/s và qua VTCB vận tốc của hệ là:
![]()
![]()
![]()

Nhớ biểu thức sau, rất hữu ích khi thi trắc nghiệm
\(W_d=n.W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{n+1}}\)
\(W_d=3W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{3+1}}=\pm\dfrac{A}{2}\)
\(\Rightarrow F_{dh}=k.\Delta l=k.\dfrac{A}{2}=\dfrac{1}{2}kA\left(N\right)\)
\(F_{dh\left(max\right)}=kA\left(N\right)\)
\(\Rightarrow\dfrac{F_{dh}}{F_{dh\left(max\right)}}=\dfrac{\dfrac{1}{2}kA}{kA}=\dfrac{1}{2}\)

Tần số góc: \(\omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{100}{0,1}}=10\pi(rad/s)\)
Biểu diễn dao động bằng véc tơ quay, tại thời điểm 7/60s thì véc tơ quay đã quay 1 góc là: \(\alpha=\omega.t=\dfrac{7}{6}\pi\)
Tại vị trí \(W_đ=3.W_t\)\(\Rightarrow W=W_đ+W_t=4W_t\)
\(\Rightarrow x=\pm\dfrac{A}{2}=\pm 2cm\)
Vì tốc độ của vật đang giảm nên có 2 trường hợp:
+ TH1: Dao động ứng với trạng thái tại M, sau khi quay \(\dfrac{7}{6}\pi\) sẽ đến biên âm --> Li độ là -4cm.
+ TH2: Dao động ứng với trạng thái N, sau khi quay \(\dfrac{7}{6}\pi\) sẽ đến biên độ dương -> Li độ là 4cm.

Công thức tính thế năng của con lắc lò xo ở li độ x:
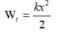
Đáp án A

Đáp án B
Vận tốc có độ lớn cực đại là 0,4m/s nên ![]()
Lúc vật đang ở vị trí x=2(cm) theo chiều dương thì tại đó động năng bằng ba lần thế năng nên:
W đ = 3 W t ⇒ 4 W t = W ⇒ 4 kx 2 2 = kA 2 2 ⇒ A = 2 x = 4 cm .
Gốc thời gian tại lúc này nên
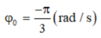
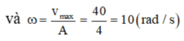
Vậy phương trình dao động của vật là: