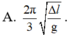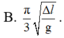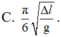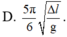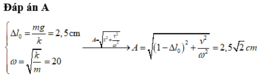Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dễ thấy A=3cm
20s dao động 50 lần => 1s dao động 2,5 lần hay f=2,5 => ω=2.pi.f = 5pi
tương tự câu 1 : ω= căn (g/Δℓo) => Δℓo = 0,04m = 4cm > 3cm
=> điểm mà lò xo không giãn nằm trên biên trên và vị trí cân bằng
vẽ hình => Δℓ[min] = 4-3=1cm, Δℓ[max] = 4+3+3=10cm
tỉ số lực đàn hồi cực đại và cực tiểu : Δℓ[max] / Δℓ[min]=10

Chọn A
Chọn trục tọa độ có phương thẳng đứng, chiều dương từ trên xuống dưới.
+ A = 2Dl
+ Vị trí thả vật là x1 = +A và vị trí lò xo không biến dạng là x2 = - Dl = -A/2.
+ Sử dụng thang thời gian:
t = tA→O + tO→- A/2
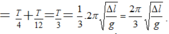

Biên độ: \(A=1cm\)
Tần số góc: \(\omega=\sqrt{\dfrac{g}{\Delta \ell_0}}=\sqrt{\dfrac{10}{0,04}}=5\pi(rad/s)\)
Lúc vừa mới thả thì vật đang ở biên, do đó gia tốc của vật là gia tốc cực đại:
\(a_{max}=\omega^2.A=(5\pi)^2.1=250(cm/s^2)\)

Tần số góc của dao động là:
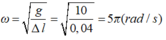
Lò xo không dãn tức là lò xo bị nén, là khoảng thời gian vật đi từ vị trí có tọa độ x = -∆l ra biên âm rồi đến vị trí x = -∆l theo chiều dương
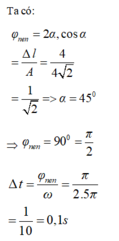
Đáp án A

Biên độ: A = 1cm
Tần số góc: \(\omega=\sqrt{\frac{g}{\Delta l_0}}=\sqrt{\frac{10}{0,04}}=5\pi\left(rad\s\right)\)
Lúc vừa mới thả thì vật đang ở biên, do đó gia tốc của vật là gia tốc cực đại:
\(a_{max}\) \(=\omega^2\) \(.A=\left(5\pi\right)^2\) \(.1=250\left(cm\s^2 \right)\)

W=√(g/dentaLo)=5√10
=>T=0,4s. Tại t=0,4/3=T/3 vật ở vt A/2=1cm. =>Fdh=KdentaL=K(dentalo-1)=3N

Đáp án A
Phương pháp: Sử dụng đường tròn lượng giác và lí thuyết về con lắc lò xo treo thẳng đứng
Cách giải:
- Độ dãn của lò xo khi vật ở vị trí cân bằng:
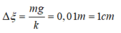
- Kéo vật xuống khỏi vị trí cân bằng theo phương thẳng đứng 2 cm rồi buông nhẹ nên biên độ dao động của vật: A = 2cm.
- Chu kỳ dao động T = 0,2s.
- Lò xo bị nén khi vật di chuyển trong đoạn từ li độ -1cm và biên âm -2cm, được biểu diễn bằng phần tô đậm như hình vẽ.
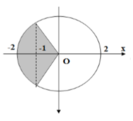
- Trong 0,5s = 2,5T, thời gian lò xo bị nén là: 2T/3 + T/6 = 1,6 (s)