Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Sử dụng lí thuyết về bài toán con lắc đơn chịu tác dụng của lực quán tính
Cách giải:
+ Khi thang máy đi lên NDĐ với gia tốc có độ lớn là a thì gia tốc trọng trường hiệu dụng : g1 = g + a
=> Chu kì dao động: T 1 = 2 π l g + a
+ Khi thang máy đi lên CDĐ với gia tốc có độ lớn là a thì gia tốc trọng trường hiệu dụng : g2 = g – a
=> Chu kì dao động T 2 = 2 π l g - a
+ Theo đề bài T 2 = 2 T 1 ⇒ π l g - a = 2 l g + a => g + a = 4(g-a) => a = 3g/5
=> Chọn C

Đáp án A
Phương pháp: Sử dụng lí thuyết về bài toán con lắc đơn chịu tác dụng của lực quán tính
Cách giải:
Theo bài ra ta có:
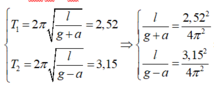
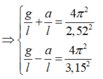
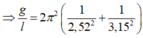
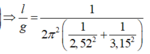
Khi thang máy đứng yên:
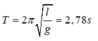

Chọn đáp án D.
Ta có T 1 = 2 π 1 g + a (1)
T 2 = 2 π 1 g − a (2)
T = 2 π 1 g (3)
Từ (1); (2) và (3) ta được 2 T 2 = 1 T 1 2 + 1 T 2 2 ⇒ T = 3 , 4 s

Chu kỳ của con lắc khi thang máy chuyển động thẳng đứng đi lên nhanh dần đều với gia tốc a là:
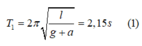
Chu kỳ của con lắc khi thang máy chuyển động thẳng đứng đi lên chậm dần đều với gia tốc a là:
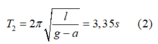
Chia (1) cho (2) ta được: a = 0,42g
Thay giá trị của a vào (1) ta được:

Với T là chu kỳ của con lắc khi thang máy không chuyển động
Đáp án C
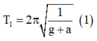
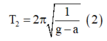
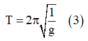
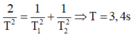
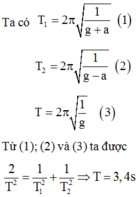
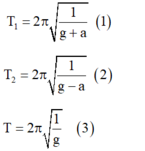
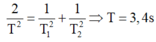
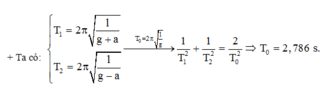

Chu kì dao động của con lắc trong hai trường hợp:
Đáp án C