Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Theo đề bài, ta có :
\(\frac{5}{x}-\frac{y}{3}=\frac{1}{6}\) => \(\frac{5}{x}=\frac{1+2y}{6}\)
| 2y+1 | 1 | -1 | 3 | -3 | 5 | -5 | 15 | -15 |
| 2y | 0 | -2 | 2 | -4 | 4 | -6 | 14 | -16 |
| y | 0 | -1 | 1 | -2 | 2 | -3 | 7 | -8 |
| x | 30 | -30 | 10 | -10 | 6 | -6 | 2 | -2 |
b) \(\frac{2}{y}-\frac{x}{6}=\frac{1}{30}\) => \(\frac{2}{y}=\frac{5x-1}{30}\)
| 5x-1 | -1 | 4 | -6 |
| 5x | 0 | 5 | -5 |
| x | 0 | 1 | -1 |
| y | -60 | 15 | -10 |

a) Vì \(\left|x\left(x^2-3\right)\right|\ge0\) nên \(x\ge0\)
Ta có : |x(x2 - 3)| = x
<=> x(x2 - 3) = x <=> x2 - 3 = x : x = 1 <=> x2 = 4
Vì x \(\ge\) 0 nên x = 2


2) Ta có:
\(B=x^4+2x^3y-2x^3+x^2y^2-2x^2y-x\left(x+y\right)+2x+3\)
\(=x^4+x^3y-2x^3+x^3y+x^2y^2-2x^2y-x\left(x+y\right)+2x+3\)
\(=\left(x^4+x^3y-2x^3\right)+\left(x^3y+x^2y^2-2x^2y\right)-\left[x\left(x+y\right)-2x\right]+3\)
Do \(x+y-2=0\Rightarrow x+y=2\)
\(\Rightarrow B=\left(x^4+x^3y-2x^3\right)+\left(x^3y+x^2y^2-2x^2y\right)-\left[2x-2x\right]+3\)
\(=x^3.\left(x+y-2\right)+x^2y\left(x+y-2\right)-0+3\)
\(=0+0+3\)
\(=3\)
Vậy \(B=3\)
1) Ta có:
\(A=x^3+x^2y-2x^2-xy-y^2+3y+x-1\)
\(=\left(x^3+x^2y-2x^2\right)-\left(xy+y^2-2y\right)+y+x-1\)
\(=x^2\left(x+y-2\right)-y\left(x+y-2\right)+\left(x+y-2\right)+1\)
\(=0+0+0+1\)
\(=1\)
Vậy \(A=1\)
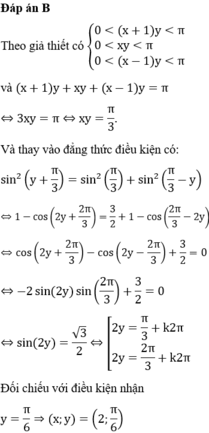

Đáp án đúng : B