Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để xác định, các ghế được đánh số từ 1 đến 10 tính từ trái sang phải.
a) Nếu các bạn nam ngồi ở các ghế ghi số lẻ thì các bạn nữ ngồi ở các ghế còn lại. Có 5! cách xếp bạn nam, 5! cách xếp bạn nữ. Tất cả có 5 ! 2 cách xếp.
Nếu các bạn nam ngồi ở các ghế ghi số chẵn, các bạn nữ ngồi ở các ghế còn lại thì có 5 ! 2 cách xếp nam và nữ.
Vậy có tất cả 2. 5 ! 2 cách xếp nam nữ ngồi xen kẽ nhau.
b) Các bạn nam được bố trí ngồi ở các ghế từ k đến k + 4, k = 1, 2, 3, 4, 5, 6. Trong mỗi trường hợp có 5 ! 2 cách xếp nam và nữ.
Vậy có 6. 5 ! 2 cách xếp mà các bạn nam ngồi cạnh nhau.

_ "Bó" các bạn nam vào một bó. (Coi bó như 1 người)
_ Xếp 1 bó bạn nam và 5 bạn nữ vào chỗ có: 6! cách.
_ Đổi chỗ trong "bó" có 5! cách
⇒ Có: 6!.5! = 86400 cách

Số cách xếp 3 nam và 3 nữ vào 6 ghế là 6! Cách.
Suy ra: \(n\left(\Omega\right)=6!=720\)
a) Ta gọi A là biến cố : “Nam, nữ ngồi xen kẽ nhau”
Ta đánh số ghế như sau:
| 1 | 2 | 3 | 4 | 5 | 6 |
Trường hợp 1:
+ Nam ngồi ghế số 1, 3, 5 suy ra có 3! cách xếp
+ Nữ ngồi ghế số 2, 4, 6 suy ra có 3! cách xếp
Suy ra trường hợp 1 có 3!.3! = 36 cách xếp
Trường hợp 2:
+ Nữ ngồi ghế số 1, 3, 5 suy ra có 3! cách xếp
+ Nam ngồi ghế số 2, 4, 6 suy ra có 3! cách xếp
Suy ra trường hợp 1 có 3!.3! = 36 cách xếp
Suy ra:
N(A) = 3!.3! + 3!.3! = 36 + 36 = 72 cách xếp.
Vậy \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{72}{720}=\dfrac{1}{10}=0,1\)
b) Gọi biến cố B: “Ba bạn nam ngồi cạnh nhau”
Xem 3 bạn nam như một phần tử N và N cùng 3 bạn nữ được xem như ngồi vào 4 ghế được đánh số như sau:
| 1 | 2 | 3 | 4 |
_ Số cách xếp N và 3 nữ vào 4 ghế là 4!
_ Mỗi cách hoán vị 3 nam cho nhau trong cùng một vị trí ta có thêm 3! cách xếp khác nhau.
Suy ra n(B) = 4!.3!=144
Vậy: \(P\left(B\right)=\dfrac{n\left(B\right)}{n\left(\Omega\right)}=\dfrac{144}{720}=\dfrac{1}{5}=0,2\)

Số cách xếp 3 nam và 3 nữ vào 6 ghế là 6! Cách.
Suy ra: n(Ω)=6!=720n(Ω)=6!=720
a) Ta gọi A là biến cố : “Nam, nữ ngồi xen kẽ nhau”
Ta đánh số ghế như sau:
|
1 |
2 |
3 |
4 |
5 |
6 |
Trường hợp 1:
+ Nam ngồi ghế số 1, 3, 5 suy ra có 3! cách xếp
+ Nữ ngồi ghế số 2, 4, 6 suy ra có 3! cách xếp
Suy ra trường hợp 1 có 3!.3! = 36 cách xếp
Trường hợp 2:
+ Nữ ngồi ghế số 1, 3, 5 suy ra có 3! cách xếp
+ Nam ngồi ghế số 2, 4, 6 suy ra có 3! cách xếp
Suy ra trường hợp 1 có 3!.3! = 36 cách xếp
Suy ra:
N(A) = 3!.3! + 3!.3! = 36 + 36 = 72 cách xếp.
Vậy P(A)=n(A)n(Ω)=72720=110=0,1P(A)=n(A)n(Ω)=72720=110=0,1
b) Gọi biến cố B: “Ba bạn nam ngồi cạnh nhau”
Xem 3 bạn nam như một phần tử N và N cùng 3 bạn nữ được xem như ngồi vào 4 ghế được đánh số như sau:
|
1 |
2 |
3 |
4 |
_ Số cách xếp N và 3 nữ vào 4 ghế là 4!
_ Mỗi cách hoán vị 3 nam cho nhau trong cùng một vị trí ta có thêm 3! cách xếp khác nhau.
Suy ra n(B) = 4!.3!=144
Vậy : P(B)=n(B)n(Ω)=144720=15=0,2

Không gian mẫu là việc sắp xếp 6 bạn vào 6 ghế tùy ý
⇒ n(Ω) = P6 = 6! = 720.
a. Gọi A: “ Nam, nữ ngồi xen kẽ nhau”
+ Chọn chỗ ngồi cho 3 bạn nữ: Có 2 cách (Vị trí 1,3,5 hoặc 2,4,6).
+ Sắp xếp 3 bạn nữ vào 3 chỗ: Có 3! = 6 cách
+ Sắp xếp 3 bạn nam vào 3 chỗ còn lại: Có 3! = 6 cách
⇒ Theo quy tắc nhân: n(A) = 2.6.6 = 72 (cách).
⇒ n(A) = 2.3!.3! = 72
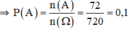
b. B: “Ban bạn nam ngồi cạnh nhau”
+ Chọn 3 chỗ ngồi cạnh nhau cho 3 bạn nam: Có 4 cách.
+ Sắp xếp 3 bạn nam vào 3 chỗ: Có 3! = 6 cách.
+ Sắp xếp 3 bạn nữ vào 3 chỗ còn lại: Có 3! = 6 cách
⇒ Theo quy tắc nhân: n(B) = 4.6.6 = 144 (cách)
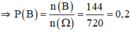
Xác suất để ba bạn nam ngồi cạnh nhau là:
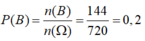

Không gian mẫu: \(8!\)
Có 2 kiểu xếp (kí hiệu N là nam, n là nữ): \(NnNnNnNn\) hoặc \(nNnNnNnN\)
Hoán vị 4 bạn nữ: \(4!\) cách
Hoán vị 4 bạn nam: \(4!\) cách
\(\Rightarrow2.4!.4!\) cách xếp thỏa mãn
Xác suất...

Đáp án là B.
• Kí hiệu số ghế là 1;2;3;4;5;6.
• Xếp trước 3 nam ngồi ở vị trí số lẻ và 3 nữ ngồi ở vị trí số chẳn và ngược lại
Ta có: 3!.3!.2! = 72

\(A:\)"Không có 2 nữ ngồi cạnh nhau"
Xếp sao cho không có 2 bạn nữ nào ngồi cạnh nhau tức nam nữ ngồi xen kẽ.
Xếp 7 bạn nam có \(7!\) cách xếp.
Giữa 7 bạn nam có 8 khoảng trống(gồm 6 khoảng trống ở giữa và 2 khoảng trống ở đầu và cuối)
Xếp 5 bạn nữ sao cho không có 2 bạn nữ nào ngồi cạnh nhau ta xếp 5 bạn nữ vào 2 trong 8 khoảng trống đó có \(A_8^5\)cách xếp.
\(\Rightarrow n\left(A\right)=7!\cdot A_8^5\) cách xếp.

Để xác định, các ghế được đánh số thứ tự từ 1 đến 10 tính từ trái sang phải.
a) Nếu các bạn nam ngồi ở các ghế ghi số lẻ thì các bạn nữ ngồi ở các ghế còn lại. Có 5! cách xếp bạn nam, 5! cách xếp bạn nữ. Tất cả có \(\left(5!\right)^2\) cách xếp
Nếu bạn nam ngồi ở các ghế ghi số chẵn, các bạn nữ ngồi ở các ghế còn lại thì có \(\left(5!\right)^2\) cách xếp nam và nữ. Vậy có tất cả \(2.\left(5!\right)^2\) cách xếp nam nữ ngồi xen kẽ nhau.
b) Các bạn nam được bố trí ngồi ở các ghế từ \(k\) đến \(k+4,k=1,2,3,4,5,6\). Trong mỗi trường hợp có \(\left(5!\right)^2\) cách xếp nam và nữ. Vậy có \(6.\left(5!\right)^2\) cách xếp mà các bạn nam ngồi cạnh nhau.
cho em hỏi khúc k+4 ạ...