Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn bị ngược rồi, B có 3 người còn A có 4 người mà. Không sao vẫn tính là bạn đang sắp xếp A nhé, mình kí hiệu 4 học sinh A là A1 A2 A3 A4 thì ở chỗ xếp học sinh A ấy bạn mới chỉ xếp cho A1, A2, A3 hoặc A4 mà thôi nên phải nhân 4 nữa. Đáp án phải là D
D.Công Thiện: Uh mình nhìn nhầm. Nhưng đáp án không thay đổi bạn ơi. Chỉ cần thay B bằng A thôi mà.

Chọn A
Xếp 6 học sinh có 6! cách xếp.
Giữa 6 học sinh có 5 khoảng trống.
Xếp 3 thầy giáo A, B, C vào 5 khoảng trống trên có: A 5 3 cách.
Vậy số cách xếp thỏa mãn yêu cầu là: 6!. A 5 3 = 43200 cách.

`n(\Omega)=6! =720`
`@TH1:` H/s lớp `C` ngồi đầu tiên hoặc cuối cùng.
`=>` Có `2.1.A_3 ^1 .4! =144` cách xếp h/s lớp `C` không ngồi cạnh lớp `B`.
`@TH2:` H/s lớp `C` không ngồi đầu cũng không ngồi cuối.
`=>` Có `4.A_3 ^2 .3! =144` cách xếp h/s lớp `C` không ngồi cạnh lớp `B`.
Gọi `A:`" H/s lớp `C` không ngồi cạnh h/s lớp `B`"
`=>n(A)=144.2=288`
`=>P(A)=288/720=2/5`
`->bb D`

Chọn D
Nhóm có tất cả 9 học sinh nên số cách xếp 9 học sinh này ngồi vào một hàng có 9 ghế là 9! = 362880(cách).
Vậy số phần tử không gian mẫu là n ( Ω ) = 362880
Đặt biến cố A: “ 3 học sinh lớp không ngồi ghế liền nhau”.
Giả sử học sinh lớp 10 ngồi 3 ghế liền nhau. Ta xem 3 học sinh này là một nhóm
+/ Xếp X và 6 bạn còn lại vào ghế có 7! cách xếp.
+/ Ứng với mỗi cách xếp ở trên, có 3! cách xếp các bạn trong nhóm X.
Vậy theo quy tắc nhân ta có số cách xếp là: 7!.3! = 30240 (cách).
Suy ra số cách xếp để học sinh lớp không ngồi cạnh nhau là (cách) .
Vậy xác suất để học sinh lớp 10 không ngồi cạnh nhau là 362880 - 30240 = 332640 (cách)
=> n(A) = 332640
Vậy xác suất để học sinh lớp 10 không ngồi cạnh nhau là
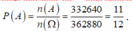

Do mỗi học sinh lớp 12 ngồi giữa hai học sinh khối 11 nên ở vị trí đầu tiên và cuối cùng của dãy ghế sẽ là học sinh khối 11.
Bước 1: Xếp 6 học sinh lớp 11 thành một hàng ngang, có 6! cách.
Bước 2: giữa 6 bạn học sinh lớp 11 có 5 khoảng trống, chọn 3 khoảng trống trong 5 khoảng trống để xếp các bạn lớp 12, có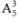 cách( có liên quan đến thứ tự).
cách( có liên quan đến thứ tự).
Theo quy tắc nhân có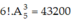 cách xếp thỏa yêu cầu.
cách xếp thỏa yêu cầu.
Chọn C.