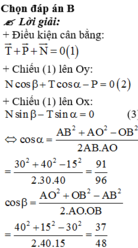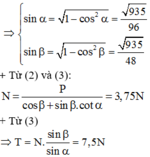Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng phương pháp tọa độ
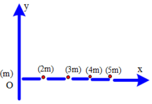
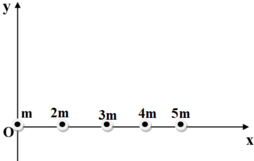
x G = 2 m l + 3 m ( 2 l ) + 4 m ( 3 l ) + 5 m ( 4 l ) 15 m x G = 8 l 3
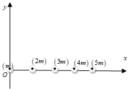

Chọn đáp án B
Gọi
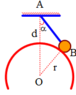
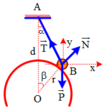
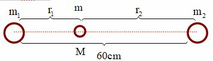
F h d 1 → là lực hấp dẫn giữa m 1 và m
F h d 2 → là lực hấp dẫn giữa m 2 và m.
+ Theo đề bài, ta có:
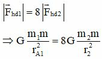
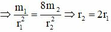 (1)
(1)
+ Từ hình vẽ ta thấy: ![]() (2)
(2)
![]()

Hệ vật "Quả cầu - Lò xo - Trái Đất" là hệ cô lập, do không chịu tác dụng các ngoại lực (lực ma sát, lực cản), chỉ có các nội lực tương tác (trọng lực, phản lực, lực đàn hồi), nên cơ năng của hệ vật bảo toàn.
Chọn vị trí cân bằng của hệ vật làm gốc tính thế năng đàn hồi, chiều lò xo bị kéo dãn là chiều dương.
- Tại vị trí ban đầu : quả cầu có vận tốc v 0 = 0 và lò xo bị kéo dãn một đoạn ∆ l 0 > 0 cm, nên cơ năng của hệ vật:
W 0 = k( ∆ l 0 )2/2
- Tại vị trí cân bằng: quả cầu có vận tốc v ≠ 0 và lò xo không bị biến dạng ( ∆ = 0), nên cơ năng của hệ vật :
W = m v 2 /2
Áp dụng định luật bảo toàn cơ năng cho chuyển động của hệ vật:
W = W 0 ⇒ m v 2 /2 = k( ∆ l 0 )2/2
Suy ra vận tốc của quả cầu khi nó về tới vị trí cân bằng:
v = ∆ l 0 k / m = 3. 10 - 2 100 / 40 . 10 - 3 = 1,5(m/s)

a)
b)Nếu tăng khoảng cách lên 2 lần thì \(F_{hd}\) giảm 4 lần.
Khi đó: \(F'_{hd}=\dfrac{2,1\cdot10^{-6}}{4}=5,25\cdot10^{-7}N\)
c)Để lực hấp dẫn giữa hai quả cầu lớn nhất thì khoảng cách giữa chúng phải nhỏ nhất.
\(F_{max}=\dfrac{G\cdot m_1m_2}{\left(2R\right)^2}\)

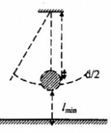
+ Vì quả cầu chuyển động đu đưa theo cung tròn nên, ta có: F - P = m α h t
↔ k . x - m g = m v 2 R ↔ E . S l 0 x - m g = m v 2 l 0 + x + D 2 ↔ E πd 2 4 l 0 x - m g ≈ m v 2 l 0 + D 2 → x = 4 l 0 m E πd 2 v 2 l 0 + D 2 + g = 4 . 2 , 8 . 4 1 , 86 . 10 11 . π . 0 , 9 . 10 - 3 2 5 2 2 , 8 + 0 , 1 2 + 10 ≈ 1 , 8 . 10 - 3 m
Khoảng trống tối thiểu từ quả cầu đến sàn là: l m i n = 3 - 2 , 8 + 0 , 1 + 0 , 0018 = 0 , 0982 m = 9 , 82 c m
Đáp án: A