Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Kí hiệu Nam: l và Nữ: ¡. Ta có
Có 2 trường hợp Nam, nữ ken kẽ nhau và 4 trường hợp hai bạn Nữ ngồi cạnh nhau.
Trường hợp 1. Nam nữ ngồi xen kẽ nhau gồm:
Nam phía trước: l¡l¡l¡l¡l¡.
Nữ phía trước: ¡l¡l¡l¡l¡l.
Trường hợp 2. Hai bạn nữ ngồi cạnh nhau: l¡¡l¡l¡l¡l Hoặc
l¡l¡¡l¡l¡l. Tương tự ta có thêm 2 trường hợp nữa. Các bước xếp như sau:
B1: Xếp 5 bạn nam. B2: Xếp cặp Tự - Trọng. B3: Xếp các bạn nữ còn lại. Khi đó số kết quả xếp cho 2 trường hợp trên như sau:


Số cách xếp ngẫu nhiên 12 học sinh thành hàng ngang là 12! cách.
Ta tìm số cách xếp thoả mãn:
Xếp hai bạn An và Bình cạnh nhau có 2! cách, gọi nhóm này là X;
Xếp 4 bạn lớp C còn lại cùng với X có 5! cách;
Lúc này có 4 vị trí (xen giữa các bạn lớp C còn lại và X) để xếp 3 bạn lớp B vào có A34A43cách;
Còn lại 3 vị trí để các bạn lớp A có thể xếp vào (1 vị trí xen giữa và ở hai đầu) có 3.3.3 cách.
Vậy có tất cả 2 ! 5 ! A 4 3 27 cách xếp thoả mãn.
Xác suất cần tính bằng 2 ! 5 ! A 4 3 27 12 ! = 1 3080
Chọn đáp án D.

Chọn B.
Phương pháp: Sử dụng hoán vị và quy tắc nhân.
Cách giải: Xếp 12 học sinh vào 12 ghế có 12! cách xếp.
Đánh số ghế như sau:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Chọn giới tính nam hoặc nữ có 2 cách.
Xếp nam hoặc nữ ngồi vào các ghế 1, 3, 5, 8, 10,12 có 6!= 720 cách.
Xếp các bạn giới tính còn lại vào 6 ghế còn lại có 6!= 720cách.
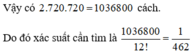

Chọn B.
Kí hiệu học sinh lớp 12A, 12B, 12C lần lượt là A, B, C.
Số phần tử không gian mẫu là n(Ω)=9!
Gọi E là biến cố các học sinh cùng lớp luôn ngồi cạnh nhau. Ta có các bước sắp xếp như sau:
- Xếp 5 học sinh lớp 12C ngồi vào bàn sao cho các học sinh này ngồi sát nhau. Số cách sắp xếp là 5!
- Xếp 3 học sinh lớp 12B vào bàn sao cho các học sinh này ngồi sát nhau và sát nhóm của học sinh 12C. Số cách sắp xếp là 3!.2
- Xếp 2 học sinh lớp 12A vào hai vị trí còn lại của bàn. Số cách sắp xếp là 2!
Số phần tử thuận lợi cho biến cố E là n(E)=5!.3!.2.2!
Xác suất của A là P ( E ) = n ( E ) n ( Ω ) = 1 126







Tìm số cách xếp ngẫu nhiên:
Chọn ra 6 trong 12 học sinh rồi xếp vào bàn dài có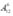 cách xếp;
cách xếp;
6 học sinh còn lại xếp vào bàn tròn có (6-1)!=5! cách xếp.
Vậy có tất cả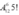 cách xếp ngẫu nhiên.
cách xếp ngẫu nhiên.
Ta tìm số cách xếp mà A, B cùng ngồi 1 bàn và ngồi cạnh nhau:
TH1: A, B ngồi cùng bàn dài và cạnh nhau có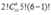 cách;
cách;
TH2: A, B ngồi cùng bàn tròn và cạnh nhau có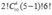 cách.
cách.
Vậy có tất cả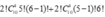 cách xếp thoả mãn.
cách xếp thoả mãn.
Xác suất cần tính bằng
Chọn đáp án B.
*Chú ý số cách xếp n học sinh vào 1 bàn tròn bằng (n−1)! cách.
Chọn đáp án B.