Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) $A=\dfrac{1}{1.2}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}$
$=>A=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}$
$=>A=(1+\dfrac{1}{3}+...+\dfrac{1}{99})-(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{100})$
$=>A=(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{99}+\dfrac{1}{100})-(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{100}.2)$
$=>A=(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{100})-(1+\dfrac{1}{2}+...+\dfrac{1}{50})$
$=>A=\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{100}$
b) Ta có : $A=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}$
$=>A=(1-\dfrac{1}{2}+\dfrac{1}{3})-(\dfrac{1}{4}-\dfrac{1}{5})-...-(\dfrac{1}{98}-\dfrac{1}{99})-\dfrac{1}{100}$
$=>A<1-\dfrac{1}{2}+\dfrac{1}{3}=\dfrac{5}{6}$

\(1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}=\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{100}\)
Đặt A= \(1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
=\(\left(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{99}+\dfrac{1}{100}\right)-2\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)\)
=\(\left(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{99}+\dfrac{1}{100}\right)-\left(1+\dfrac{1}{2}+...+\dfrac{1}{50}\right)\)
= \(\left(\dfrac{1}{51}+\dfrac{1}{52}+\dfrac{1}{53}+...+\dfrac{1}{100}\right)\)

Ta có :
\(\dfrac{1}{5^2}< \dfrac{1}{4.5}\)
\(\dfrac{1}{6^2}< \dfrac{1}{5.6}\)
....................
\(\dfrac{1}{100^2}< \dfrac{1}{99.100}\)
\(\Leftrightarrow\dfrac{1}{5^2}+\dfrac{1}{6^2}+........+\dfrac{1}{100^2}< \dfrac{1}{4.5}+\dfrac{1}{5.6}+.....+\dfrac{1}{99.100}=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+.....+\dfrac{1}{99}-\dfrac{1}{100}=\dfrac{1}{4}-\dfrac{1}{100}< \dfrac{1}{4}\left(1\right)\)
Lại có :
\(\dfrac{1}{5^2}>\dfrac{1}{5.6}\)
\(\dfrac{1}{6^2}>\dfrac{1}{6.7}\)
............
\(\dfrac{1}{100^2}>\dfrac{1}{100.101}\)
\(\Leftrightarrow\dfrac{1}{5^2}+\dfrac{1}{6^2}+......+\dfrac{1}{100^2}>\dfrac{1}{5.6}+\dfrac{1}{6.7}+.....+\dfrac{1}{100.101}=\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+.....+\dfrac{1}{100}-\dfrac{1}{101}=\dfrac{1}{5}-\dfrac{1}{101}>\dfrac{1}{6}\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrowđpcm\)

- Ta có : `C=51/2 * 52/2 * 53/2* ... * 100/2`
`-> C=(51.52.53...100)/(2^50)`
`-> C=((1.2.3...50).(51.52.53...100))/((1.2.3...50).2^50)`
`-> C=(1.2.3...100)/((1.2).(2.2).(3.2)...(50.2))`
`-> C=(1.2.3...100)/(2.4.6...100)`
`-> C=1.3.5.7...99`
- Từ đó ta có :
`B-C=1.3.5.7...99-1.3.5.7...99=0`
- Vậy `B-C=0`
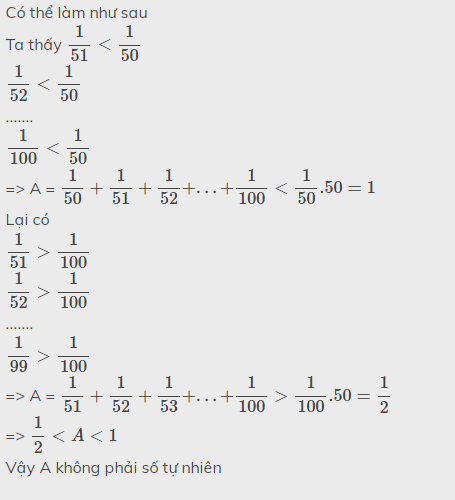
Đặt \(A=\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{100}\)
Ta có: \(\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{75}>\dfrac{1}{75}+\dfrac{1}{75}+...+\dfrac{1}{75}=\dfrac{25}{75}=\dfrac{1}{3}\)
\(\dfrac{1}{76}+\dfrac{1}{77}+...+\dfrac{1}{100}>\dfrac{1}{100}+\dfrac{1}{100}+...+\dfrac{1}{100}=\dfrac{25}{100}=\dfrac{1}{4}\)
Do đó: \(A>\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{7}{12}\)(1)
Ta có: \(\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{75}< \dfrac{1}{50}+\dfrac{1}{50}+...+\dfrac{1}{50}=\dfrac{25}{50}=\dfrac{1}{2}\)
\(\dfrac{1}{76}+\dfrac{1}{77}+...+\dfrac{1}{100}< \dfrac{1}{75}+\dfrac{1}{75}+...+\dfrac{1}{75}=\dfrac{25}{75}=\dfrac{1}{3}\)
Do đó: \(A< \dfrac{1}{2}+\dfrac{1}{3}=\dfrac{5}{6}\)(2)
Từ (1) và (2) ta suy ra ĐPCM