Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

trên tia đối của tia MA lấy điểm D sao cho MD = MA
xét \(\Delta AMB\)và \(\Delta DMC\)có :
MB = MC ( gt )
\(\widehat{M_1}=\widehat{M_2}\)( hai góc đối đỉnh )
MA = MD ( do cách vẽ )
Suy ra : \(\Delta AMB\)= \(\Delta DMC\)( c.g.c )
Suy ra : AB = AC và \(\widehat{A_1}=\widehat{D}\) \(\Rightarrow\)AB // CD ( vì có cặp góc sole trong bằng nhau )
vì \(AC\perp AB\)( gt ) nên AC \(\perp\)CD ( quan hệ giữa tính song song và vuông góc )
Xét \(\Delta ABC\)và \(\Delta CDA\)có :
AB = CD ( chứng minh trên )
\(\widehat{A}=\widehat{C}=90^o\)
AC ( chung )
Vậy \(\Delta ABC\)= \(\Delta CDA\)( c.g.c ) suy ra BC = AD
vì \(AM=MD=\frac{AD}{2}\)nên \(AM=\frac{BC}{2}\)

Tam giác vuông ABC, vuông tại A, có AM là trung tuyến
trên tia đối của MA lấy điểm D sao cho MD=AM
Do đó AM=1/2 AD (1)
suy ra tứ giác ABDC là hình bình hành, có ^A=90*
nên ABDC là hình chữ nhật
suy ra AD=BC (2)
Từ (1) và (2) ta có AM = 1/2 BC
Vậy trong 1 tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Chúc thành công
Tam giác vuông ABC, vuông tại A, có AM là trung tuyến
trên tia đối của MA lấy điểm D sao cho MD=AM
Do đó AM=1/2 AD (1)
suy ra tứ giác ABDC là hình bình hành, có ^A=90*
nên ABDC là hình chữ nhật
suy ra AD=BC (2)
Từ (1) và (2) ta có AM = 1/2 BC
Vậy trong 1 tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.

Vì tâm đường tròn đi qua 3 đỉnh của tam giác với mỗi tam giác chỉ có duy nhất 1 điểm.
Gọi I là trung điểm cạnh huyển BC của tam giác ABC vuông tại A.
Ta sẽ đi chứng minh I là tâm đường tròn đi qua 3 đỉnh tam giác ABC.
Thật vậy, trên tia đối tia IA , ta lấy điểm D sao cho IA=ID .
Vì I là trung điểm BC => IB=IC
Xét tam giác AIB và tam giác CID có:
AI=IC ; BI=ID ; AIB =CID (2 góc đối đỉnh)
=> Tam giác AIB =tam giác CID (c.g.c)
=> AB=CD; IAB = ICD
Vì IAB =ICD , mà 2 góc này ở vị trí so le trong
=> AB// CD Mà AB vuông góc với AC
=> CD vuông góc AC => ACD = 90
Xét tam giác BAC và DCA có:
AC chung ; AB=DC ; BAC = DCA =90
=> BAC = DCA(c.g.c)
=> BC = DA
Mà IB = IC = BC/2; AI=ID =DA/2
=> IB=IC=IA
=> I là tâm đường tròn đi qua A,B, C

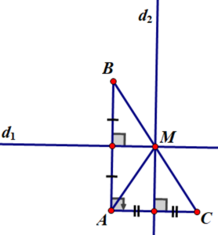
+ Giả sử ∆ABC vuông tại A.
d1 là đường trung trực cạnh AB, d2 là đường trung trực cạnh AC.
d1 cắt d2 tại M. Khi đó M là điểm cách đều ba đỉnh của tam giác ABC.
+ Áp dụng kết quả bài 55 ta có B, M, C thẳng hàng.
QUẢNG CÁO+ M cách đều A, B, C ⇒ MB = MC ⇒ M là trung điểm của cạnh BC (đpcm)
+ M là trung điểm của cạnh BC (đpcm)
*) Giả sử AM là trung tuyến của tam giác ABC suy ra M là trung điểm của cạnh BC
⇒ MB = MC = BC/2
Mà MA = MB = MC (cmt)
⇒ MA = BC/2
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.
Trên tia đối của tia MA, lấy điểm D sao cho M là trung điểm của AD
Xét ΔABM và ΔCDM có
MA=MD(M là trung điểm của AD)
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔABM=ΔCDM(c-g-c)
⇒AB=CD(hai cạnh tương ứng) và \(\widehat{A_1}=\widehat{D_1}\)(hai góc tương ứng)
Ta có: \(\widehat{A_1}+\widehat{A_2}=\widehat{BAC}=90^0\)(tia AM nằm giữa hai tia AB,AC)
hay \(\widehat{D_1}+\widehat{A_2}=90^0\)(vì \(\widehat{A_1}=\widehat{D_1}\))
Xét ΔCDA có \(\widehat{D_1}+\widehat{A_2}=90^0\)(cmt)
nên ΔCDA vuông tại C(định lí đảo của tam giác vuông)
⇒\(\widehat{ACD}=90^0\)
Xét ΔABC vuông tại A và ΔCDA vuông tại C có
AC chung
AB=CD(cmt)
Do đó: ΔABC=ΔCDA(hai cạnh góc vuông)
⇒BC=AD(hai cạnh tương ứng)
mà \(AM=MD=\frac{AD}{2}\)(M là trung điểm của AD)
nên \(AM=\frac{BC}{2}\)(đpcm)
Cảm ơn bạn!😁😁😁