Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

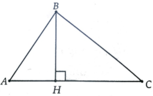
A) Vẽ t/g ABC (A là góc nhọn), đường cao BH.
1/2.AB.AC.sinA = 1/2.AB.AC.(BH/AB) = 1/2.BH.AC = S(ABC)

a, Giả sử tam giác ABC có A ^ < 90 0 kẻ đường cáo BH. Ta có BH=AB.sin A ^
=> S ∆ A B C = 1 2 A C . B H = 1 2 A B . A C . sin A
b, Giả sử tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O có
A
O
B
^
=
α
<
90
0
. Kẻ AH
⊥
BD, tại H và CK
⊥
BD tại K
Ta có: AH = OA.sinα
=> S A B D = 1 2 B D . A H = 1 2 B D . O A . sin α
Tương tự: S C B D = 1 2 B D . C K = 1 2 B D . O C . sin α
=> S A B C D = S A B D + S C B D = 1 2 B D . O A . sin α + 1 2 B D . O C . sin α = 1 2 B D . A C . sin α


Gọi Tam giác ABC cho dẽ làm . Kẻ AH vg BC
Tam giác AHB vuông tại H , theo HT giữa cạnh và góc :
AH = AB .sin B
Ta có : \(S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}AB.sinB.BC\)

Bài 1:
Xét ΔABC vuông tại A có \(AC^2=CH\cdot CB\)
=>CH(CH+9)=400
=>CH=16cm
BC=BH+CH=25cm
\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)

Gọi AH và AK lần lượt là 2 đường cao của \(\Delta ADE\)và \(\Delta ABC\)
Xét tứ giác BCDE có \(\widehat{BEC}=\widehat{BDC}=90^o\)nên tứ giác BCDE nội tiếp
\(\Rightarrow\widehat{AED}=\widehat{ACB}\)( cùng bù với \(\widehat{BED}\))
\(\Rightarrow\Delta ADE\approx\Delta ABC\left(g.g\right)\) ( nếu chưa học tứ giác nội tiếp thì có thể xét các tam giác đồng dạng để c.m nha )
\(\Rightarrow\frac{AD}{AB}=\frac{DE}{BC}=\frac{AH}{AK}\) ( vì tỉ số đồng dạng bằng tỉ số đường cao )
a) Ta có : \(\frac{S_{ADE}}{S_{ABC}}=\frac{\frac{DE.AH}{2}}{\frac{BC.AK}{2}}=\frac{AD}{AB}.\frac{AH}{AK}=\left(\frac{AD}{AB}\right)^2\)
Mà \(\cos A=\frac{AD}{AB}\Rightarrow\cos^2=\left(\frac{AD}{AB}\right)^2\)\(\Rightarrow\frac{S_{ADE}}{S_{ABC}}=\cos^2A\)
\(\Rightarrow S_{ADE}=S_{ABC}.\cos^2A\)
b) \(S_{BCDE}=S_{ABC}-S_{ADE}=S_{ABC}.\left(1-\cos^2A\right)=S_{ABC}.\sin^2A\)( vì \(\cos^2A+\sin^2A=1\))