
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\left(2x-4\right)\left(3x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2x-4=0\\3x+5=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=4\\3x=-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{5}{3}\end{matrix}\right.\)
Vậy: \(x\in\left\{2;-\dfrac{5}{3}\right\}\).


giả sử AI kéo dài cắt BC tại D.
ta có: \(\frac{BD}{CD}=\frac{c}{b}\Rightarrow BD=\frac{c}{b}CD\Leftrightarrow\overrightarrow{DB}=-\frac{c}{b}\overrightarrow{DC}\Leftrightarrow\overrightarrow{DI}+\overrightarrow{IB}=-\frac{c}{b}\left(\overrightarrow{DI}+\overrightarrow{IC}\right)\Leftrightarrow\left(1+\frac{c}{b}\right)\overrightarrow{DI}=-\overrightarrow{IB}-\frac{c}{b}\overrightarrow{IC}\Leftrightarrow\overrightarrow{ID}=\frac{b}{b+c}\overrightarrow{IB}+\frac{c}{b+c}\overrightarrow{IC}\)
tiếp: Xét tam giác ABD có ID/IA = BD/AB= (ac/b+c)/c=a/b+c
=> ID=(a/b+c)IA
=> \(\overrightarrow{ID}=-\frac{a}{b+c}\overrightarrow{IA}\)
Thế vào (1) ta đc:
\(-\frac{a}{b+c}\overrightarrow{IA}=\frac{b}{b+c}\overrightarrow{IB}+\frac{c}{b+c}\overrightarrow{IC}\)
\(\Leftrightarrow\frac{1}{b+c}\left(a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}\right)=0\)
<=> \(a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=0\): đpcm

\(\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NC}+\overrightarrow{BM}+\overrightarrow{MN}+\overrightarrow{ND}\)
\(=2\overrightarrow{MN}+\left(\overrightarrow{AM}+\overrightarrow{BM}\right)+\left(\overrightarrow{NC}+\overrightarrow{ND}\right)=2\overrightarrow{MN}\)


Lời giải:
ĐKXĐ: $0\leq x\leq 4$
Để phương trình có nghiệm trước tiên \(m\geq0\)
Ta có \(\sqrt{x}+\sqrt{4-x}=m\Rightarrow 4+2\sqrt{x(4-x)}=m^2\)
\(\Leftrightarrow x(4-x)=\left(\frac{m^2-4}{2}\right)^2\Leftrightarrow x^2-4x+\left(\frac{m^2-4}{2}\right)^2=0\) $(1)$
Trước tiên, để $(1)$ có nghiệm thì \(\Delta'=4-\left(\frac{m^2-4}{2}\right)^2\geq 0\Leftrightarrow \sqrt{8}\geq m\)
Ta thấy PT $(1)$ có xảy ra 2TH: có một nghiệm kép hoặc hai nghiệm đều dương. Nếu PT $(1)$ có hai nghiệm đều dương thì đồng nghĩa với phương trình ban đầu cũng có hai nghiệm dương (không thỏa mãn). Do đó PT đã cho có nghiệm duy nhất khi PT $(1)$ có nghiệm kép, hay \(\Delta =0\Leftrightarrow m=\sqrt{8}\)
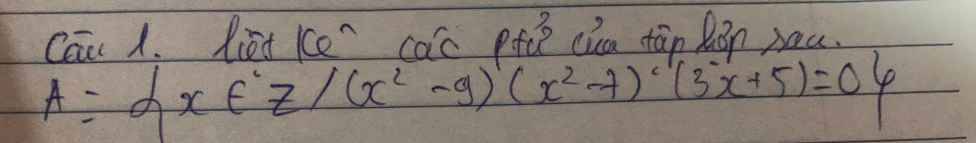 cíu bé vs mn ơi
cíu bé vs mn ơi


\(A=\left\{x\in Z|\left(x^2-9\right)\left(x^2-7\right)\left(3x+5\right)=0\right\}\)
Giải pt \(\left(x^2-9\right)\left(x^2-7\right)\left(3x+5\right)=0\) \(\left(dk:x\in Z\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-9=0\\x^2-7=0\\3x+5=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\pm3\left(tm\right)\\x=\pm\sqrt{7}\left(ktm\right)\\x=-\dfrac{5}{3}\left(ktm\right)\end{matrix}\right.\)
Vậy \(A=\left\{-3;3\right\}\)
cơn cậu mà cậu làm nốt câu B ở trang tớ hộ tớ đc k ạ