Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{\left(sina+cosa\right)^2-\left(sina-cosa\right)^2}{sina.cosa}=4\\ VT=\dfrac{sin^2a+2sinacosa+cos^2a-sin^2a+2sinacosa-cos^2a}{sinacosa}\\ =\dfrac{4sinacosa}{sinacosa}=4=VP\)
a: \(S=cos^2a\left(1+tan^2a\right)=cos^2a\cdot\dfrac{1}{cos^2a}=1\)
b: \(VP=\dfrac{1+sin2a-1+sin2a}{\dfrac{1}{2}\cdot sin2a}=\dfrac{2\cdot sin2a}{\dfrac{1}{2}\cdot sin2a}=4=VT\)

Hướng dẫn giải:
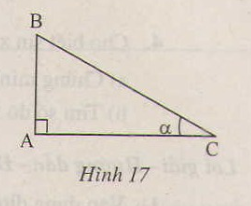
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khá
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khác.

a/ \(A=\frac{cot^2a-cos^2a}{cot^2a}-\frac{sina.cosa}{cota}\)
\(=\frac{\frac{cos^2a}{sin^2a}-cos^2a}{\frac{cos^2a}{sin^2a}}-\frac{sina.cosa}{\frac{cosa}{sina}}\)
\(=\left(1-sin^2a\right)-sin^2a=1\)
b/ \(B=\left(cosa-sina\right)^2+\left(cosa+sina\right)^2+cos^4a-sin^4a-2cos^2a\)
\(=cos^2a-2cosa.sina+sin^2a+cos^2a+2cosa.sina+sin^2a+\left(cos^2a+sin^2a\right)\left(cos^2a-sin^2a\right)-2cos^2a\)
\(=2+\left(cos^2a-sin^2a\right)-2cos^2a\)
\(=2-sin^2a-cos^2a=2-1=1\)

Đề sai em
Đề đúng: \(\dfrac{\left(sina+cosa\right)^2-\left(sina-cosa\right)^2}{sina.cosa}=4\)

Câu 1:
\(\cos a=\sqrt{1-0.28^2}=\dfrac{24}{25}\)
\(\tan a=\dfrac{0.28}{0.96}=\dfrac{7}{24}\)
\(\cot a=\dfrac{1}{\tan a}=\dfrac{24}{7}\)
\(\left(\sin a+\cos a\right)^2=\sin^2a+\cos^2a+2\cdot\sin a\cdot\cos a\)
\(=1+2\cdot\sin a\cdot\cos a\)
\(=\tan^2a\cdot\cot^2a+2\cdot\sin a\cdot\cos a\)