LT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 2 2020
Chứng minh rằng : Tích của hai số tự nhiên liên tiếp chia hết cho 2
a và b là 2 số tự nhiên liên tiếp
✽ Nếu a là chẵn, b là lẻ
⇒ a ⋮ 2 ⇒ a . b ⋮ 2
✽ Nếu a là lẻ, b là chẵn
⇒ b ⋮ 2 ⇒ a . b ⋮ 2
➤ Vậy a . b chia hết cho 2
Chứng minh rằng : Tích của 3 số tự nhiên liên tiếp chia hết cho 6
Gọi 3 số tự nhiên liên tiếp là a; a + 1; a + 2
☛ Chứng minh 3 số tự nhiên liên tiếp chia hết cho 3
✽ Nếu a chia hết 3
⇒ Tích ba số tự nhiên liên tiếp chia hết cho 3
✽ Nếu a chia cho 3 dư 1
⇒ a + 2 chia hết cho 3
⇒ Tích ba số tự nhiên liên tiếp chia hết cho 3
✽ Nếu a chia cho 3 dư 2
⇒ a + 1 chia hết cho 3
⇒ Tích ba số tự nhiên liên tiếp chia hết cho 3
☛ Chứng minh 3 số tự nhiên liên tiếp chia hết cho 2
✽ Nếu a chia hết 2
⇒ Tích ba số tự nhiên liên tiếp chia hết cho 2
✽ Nếu a chia cho 2 dư 1
⇒ a + 1 chia hết cho 2
⇒ Tích ba số tự nhiên liên tiếp chia hết cho 2
Tích ba số tự nhiên liên tiếp chia hết cho 2 và 3
➤ Tích ba số tự nhiên liên tiếp chia hết cho 6
16 tháng 8 2018
\(3+3^2+3^3+...+3^{60}\)
\(=3\cdot\left(1+3+3^2\right)+3^4\cdot\left(1+2+3^2\right)+...+3^{58}\cdot\left(1+3+3^2\right)\)
\(=3\cdot13+3^4\cdot13+...+3^{58}\cdot13\)
\(=13\cdot\left(3+3^4+...+3^{58}\right)⋮13\left(đpcm\right)\)
DQ
2
T
26 tháng 9 2023
\(P=3^{10}+3^{11}+3^{12}\)
\(=3^{10}\cdot\left(1+3+3^2\right)\)
\(=3^{10}\cdot13\)
Vì \(13⋮13\) nên \(3^{10}\cdot13⋮13\)
hay \(P⋮13\)
Vậy ...
#\(Toru\)
KV
26 tháng 9 2023
P = 3¹⁰ + 3¹¹ + 3¹²
= 3¹⁰.(1 + 3 + 3²)
= 3¹⁰ . 13 ⋮ 13
Vậy P ⋮ 13
N
7 tháng 10 2016
Câu hỏi của Nguyễn Nhật Loan - Toán lớp 6 - Học toán với OnlineMath
7 tháng 10 2016
Ta có: A= 2 + 22 + 23 + ... + 260= (2 +22) + (23+ 24) + ... + (259 + 260).
= 2 x (2 + 1) + 23 x (2 + 1) + ... + 259 x (2 + 1).
= 2 x 3 + 23 x 3 + ... + 259 x 3.
= 3 x ( 2 + 23 + ... + 259).
Vì A = 3 x ( 2 + 23 + ... + 259) nên A chia hết cho 3.
A= (2 +22 + 23) + (24 + 25 + 26) + ... + (258 + 259 + 260).
= 2 x (1 + 2 + 22) + 24 x (1 + 2 + 22) + ... + 258 x (1 + 2 + 22).
= 2 x 7 + 24 x 7 + ... + 258 x 7.
= 7 x ( 2 + 24 + ... + 258).
Vì A = 7 x ( 2 + 24 + ... + 258) nên A chia hết cho 7.
A= (2 +22 + 23 + 24) + (25 + 26 + 27 + 28) + ... + (257 + 258 + 259 + 260).
= 2 x (1 + 2 + 22 + 23) + 25 x (1 + 2 + 22 + 23) + ... + 257 x (1 + 2 + 22 + 23).
= 2 x 15 + 25 x 15 + ... + 257 x 15.
= 15 x ( 2 + 24 + ... + 258).
Vì A = 15 x ( 2 + 24 + ... + 258) nên A chia hết cho 15.
Ta có: B= 3 + 33 + 35 + ... + 31991= (3 + 33 + 35) + (37+ 39 + 311 ) + ... + (31987 + 31989 + 31991).
= 3 x (1 + 32 + 34) + 37 x (1 + 32 + 34) + ... + 31987 x (1 + 32 + 34).
= 3 x 91 + 37 x 91 + ... + 31987 x 91= 3 x 7 x 13 + 37 x 7 x 13 + ... + 31987 x 7 x 13.
= 13 x ( 3 x 7 + 37 x 7 + ... + 31987 x 7).
Vì B = 13 x ( 3 x 7 + 37 x 7 + ... + 31987 x 7) nên B chia hết cho 13.
B= (3 + 33 + 35 + 37) + ... + (31985 + 31987 + 31989 + 31991).
= 3 x (1 + 32 + 34 + 36) + ... + 31985 x (1 + 32 + 34 + 36).
= 3 x 820 + ... + 31985 x 820= 3 x 20 x 41 + ... + 31985 x 20 x 41.
= 41 x ( 3 x 20 + .. + 31985 x 20)
Vì B =41 x ( 3 x 20 + .. + 31985 x 20) nên B chia hết cho 41.
9 tháng 8 2014
Ta có: A= 2 + 22 + 23 + ... + 260= (2 +22) + (23+ 24) + ... + (259 + 260).
= 2 x (2 + 1) + 23 x (2 + 1) + ... + 259 x (2 + 1).
= 2 x 3 + 23 x 3 + ... + 259 x 3.
= 3 x ( 2 + 23 + ... + 259).
Vì A = 3 x ( 2 + 23 + ... + 259) nên A chia hết cho 3.
A= (2 +22 + 23) + (24 + 25 + 26) + ... + (258 + 259 + 260).
= 2 x (1 + 2 + 22) + 24 x (1 + 2 + 22) + ... + 258 x (1 + 2 + 22).
= 2 x 7 + 24 x 7 + ... + 258 x 7.
= 7 x ( 2 + 24 + ... + 258).
Vì A = 7 x ( 2 + 24 + ... + 258) nên A chia hết cho 7.
A= (2 +22 + 23 + 24) + (25 + 26 + 27 + 28) + ... + (257 + 258 + 259 + 260).
= 2 x (1 + 2 + 22 + 23) + 25 x (1 + 2 + 22 + 23) + ... + 257 x (1 + 2 + 22 + 23).
= 2 x 15 + 25 x 15 + ... + 257 x 15.
= 15 x ( 2 + 24 + ... + 258).
Vì A = 15 x ( 2 + 24 + ... + 258) nên A chia hết cho 15.
Ta có: B= 3 + 33 + 35 + ... + 31991= (3 + 33 + 35) + (37+ 39 + 311 ) + ... + (31987 + 31989 + 31991).
= 3 x (1 + 32 + 34) + 37 x (1 + 32 + 34) + ... + 31987 x (1 + 32 + 34).
= 3 x 91 + 37 x 91 + ... + 31987 x 91= 3 x 7 x 13 + 37 x 7 x 13 + ... + 31987 x 7 x 13.
= 13 x ( 3 x 7 + 37 x 7 + ... + 31987 x 7).
Vì B = 13 x ( 3 x 7 + 37 x 7 + ... + 31987 x 7) nên B chia hết cho 13.
B= (3 + 33 + 35 + 37) + ... + (31985 + 31987 + 31989 + 31991).
= 3 x (1 + 32 + 34 + 36) + ... + 31985 x (1 + 32 + 34 + 36).
= 3 x 820 + ... + 31985 x 820= 3 x 20 x 41 + ... + 31985 x 20 x 41.
= 41 x ( 3 x 20 + .. + 31985 x 20)
Vì B =41 x ( 3 x 20 + .. + 31985 x 20) nên B chia hết cho 41.
20 tháng 12 2014
Ta có: A= 2 + 22 + 23 + ... + 260= (2 +22) + (23+ 24) + ... + (259 + 260).
= 2 x (2 + 1) + 23 x (2 + 1) + ... + 259 x (2 + 1).
= 2 x 3 + 23 x 3 + ... + 259 x 3.
= 3 x ( 2 + 23 + ... + 259).
Vì A = 3 x ( 2 + 23 + ... + 259) nên A chia hết cho 3.
A= (2 +22 + 23) + (24 + 25 + 26) + ... + (258 + 259 + 260).
= 2 x (1 + 2 + 22) + 24 x (1 + 2 + 22) + ... + 258 x (1 + 2 + 22).
= 2 x 7 + 24 x 7 + ... + 258 x 7.
= 7 x ( 2 + 24 + ... + 258).
Vì A = 7 x ( 2 + 24 + ... + 258) nên A chia hết cho 7.
A= (2 +22 + 23 + 24) + (25 + 26 + 27 + 28) + ... + (257 + 258 + 259 + 260).
= 2 x (1 + 2 + 22 + 23) + 25 x (1 + 2 + 22 + 23) + ... + 257 x (1 + 2 + 22 + 23).
= 2 x 15 + 25 x 15 + ... + 257 x 15.
= 15 x ( 2 + 24 + ... + 258).
Vì A = 15 x ( 2 + 24 + ... + 258) nên A chia hết cho 15.
Ta có: B= 3 + 33 + 35 + ... + 31991= (3 + 33 + 35) + (37+ 39 + 311 ) + ... + (31987 + 31989 + 31991).
= 3 x (1 + 32 + 34) + 37 x (1 + 32 + 34) + ... + 31987 x (1 + 32 + 34).
= 3 x 91 + 37 x 91 + ... + 31987 x 91= 3 x 7 x 13 + 37 x 7 x 13 + ... + 31987 x 7 x 13.
= 13 x ( 3 x 7 + 37 x 7 + ... + 31987 x 7).
Vì B = 13 x ( 3 x 7 + 37 x 7 + ... + 31987 x 7) nên B chia hết cho 13.
B= (3 + 33 + 35 + 37) + ... + (31985 + 31987 + 31989 + 31991).
= 3 x (1 + 32 + 34 + 36) + ... + 31985 x (1 + 32 + 34 + 36).
= 3 x 820 + ... + 31985 x 820= 3 x 20 x 41 + ... + 31985 x 20 x 41.
= 41 x ( 3 x 20 + .. + 31985 x 20)
Vì B =41 x ( 3 x 20 + .. + 31985 x 20) nên B chia hết cho 41.
10 tháng 10 2021
\(B=2+2^2+2^3+...+2^{60}\)
\(=2\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)
\(=7\cdot\left(2+...+2^{58}\right)⋮7\)
NP
Cho A = 1^1 + 2^5 + 3^9 + 4^13 + ... + 504^2013 + 505^2017. Chứng minh A chia hết cho 5. Giúp mk với
2
R
28 tháng 12 2021
Ta có :
\(A=1+2^5+4^{13}+.....+504^{2013}+505^{2017}\)
\(A=1^{4.0+1}+2^{4.1+1}+3^{4.2+1}+....+505^{4503+1}+505^{4504+1}\)
Gọi các số nhân lên cùng 4 ở hàng số mũ là x
Xét các mũ ,ta có :
Chữ số tận cùng A sẽ là tổng của :
\(1+2+3+...+504+505\)
\(=\dfrac{\left(505+1\right).505}{2}=\dfrac{255530}{2}=127765\)
Tổng đó có chữ số tận cùng là 5
⇒⇒ Chữ số tận cùng của A là 5
Vậy chữ số tận cùng của A là 5
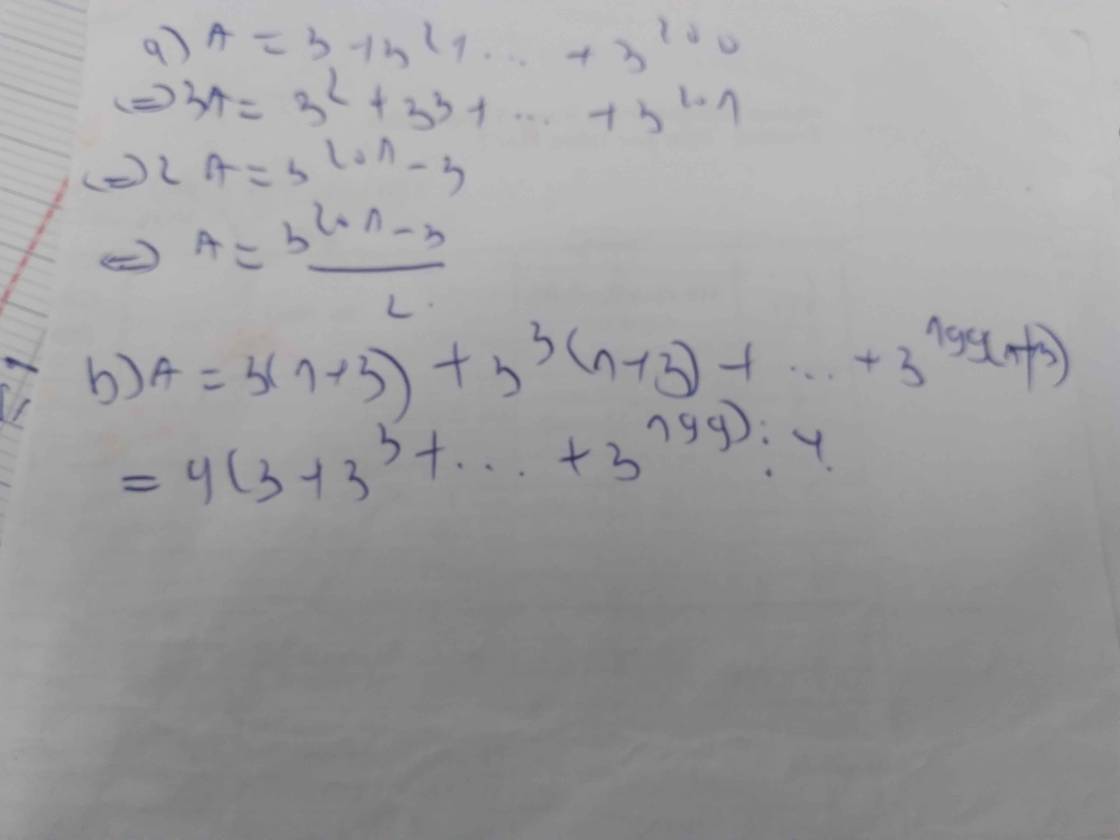
T=(3+32+33)+.....+(37+38+39)
T=3(1+3+32)+......+37(1+3+32)
T=3.13+...+37.13
T=13( 3+37) chia het cho 13
mk nha
Hinh nhu sai de rui ban