DH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
8 tháng 6 2021
Theo cách đặt giao của AC, BD là O của bạn Khôi thì phần 1 có thể CM như sau:
Áp dụng công thức BĐT trong tam giác thì:
\(AD< AO+OD\)
\(BC< BO+OC\)
Cộng theo vế 2 BĐT trên:
\(AD+BC< AO+CO+BO+DO=AC+BD\)
AH
Akai Haruma
Giáo viên
8 tháng 6 2021
Còn đoạn "Theo câu 1 thì AC < p và BD < p$ là không có cơ sở em nhé.
CM
8 tháng 5 2019
Đặt p = AB + BC + CD + DA
Ta có: OA + OD > AD (1)
OA + OB > AB (2)
OB + OC > BC (3)
OC + OD > CD (4)
Cộng vế theo vế (1), (2), (3), (4) ta có:
2(OA + OB + OC + OD) > AB + BC + CD + DA
2(AC + BD) > p
AC + BD > p/2 (*)
Mặt khác: Trong ΔABC có AC < AB + BC (5)
Trong ΔACD có AC < AD + CD (6)
Cộng vế theo vế (5) và (6) ta có:
2AC < AB + BC + CD + DA
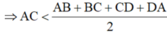
Tương tự ta cũng có BD < p/2. Suy ra: AC + BC < (p/2) + (p/2)
Hay AC + BD < p (**)
Từ (*) và (**) ta có: (p/2) < AC + BD < p.
27 tháng 7 2020
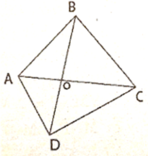
Gọi O là giao điểm của AC và BD.Ta có :
OA + OB > AB , OB + OC > AC ; OC + CD > CD , OD + OA > AD.Cộng từng vế các bất đẳng thức trên rồi chia cho 2 ,ta được \(AC+BD>\frac{AB+BC+CD+AD}{2}\)
Vậy tổng hai đường chéo lớn hơn nửa chu vi
Kết hợp : AC + BD < AB + BC + CD + DA
Vậy \(\frac{AB+BC+CD+AD}{2}< AC+BD< AB+BC< CD+DA\)
7 tháng 7 2023
Gọi O là giao của AC và BD
AB>AO+BO
AD>AO+DO
BC>BO+CO
DC>DO+CO
=>AB+AD+BC+CD>2(AC+BD)
=>(AC+BD)<P/2
AC<AB+BC
AC<AD+DC
BD<BC+CD
BD<AB+AD
=>2(AC+BD)<2*C ABCD
=>AC+BD<C ABCD
DE
16 tháng 8 2019
Gọi O là giao điểm 2 dường chéo AC và BD của tứ giác ABCD.
Áp dụng định lý " trong một tam giác một cạnh thì bé hơn tổng 2 cạnh kia" ta có:
AB < OA + OB (1)
BC < OB + OC (2)
CD < OC + OD (3)
DA < OD + OA (4)
(1) + (2) + (3) + (4) :
AB + BC + CD + DA < 2(OA + OC + OB + OD) = 2(AC + BD)
hay (1/2)(AB + BC + CD + DA) < AC + BD (*)
Mặt khác :
AC < AB + BC (1')
BD < BC + CD (2')
AC < CD + DA (3')
BD < DA + AB (4')
(1') + (2') + (3') + (4') :
2(AC + BD) > 2(AB + BC + CD + DA)
hay AC + BD < AB + BC + CD + DA (**)
Từ (*) và (**) (1/2)(AB + BC + CD + DA) < AC + BD < AB + BC + CD + DA
16 tháng 8 2019
Gọi O là giao điểm 2 dường chéo AC và BD của tứ giác ABCD.
Áp dụng định lý " trong một tam giác một cạnh thì bé hơn tổng 2 cạnh kia" ta có:
AB < OA + OB (1)
BC < OB + OC (2)
CD < OC + OD (3)
DA < OD + OA (4)
(1) + (2) + (3) + (4) :
AB + BC + CD + DA < 2(OA + OC + OB + OD) = 2(AC + BD)
hay (1/2)(AB + BC + CD + DA) < AC + BD (*)
Mặt khác :
AC < AB + BC (1')
BD < BC + CD (2')
AC < CD + DA (3')
BD < DA + AB (4')
(1') + (2') + (3') + (4') :
2(AC + BD) > 2(AB + BC + CD + DA)
hay AC + BD < AB + BC + CD + DA (**)
Từ (*) và (**) (1/2)(AB + BC + CD + DA) < AC + BD < AB + BC + CD + DA
Chúc bạn học tốt !!!
giả sử tứ giác đó có tên là abcd, gọi o là giao điểm của hai đường chéo ac và bd
Áp dụng BĐT tam giác(học ở lớp 7) ta có:
AO+OB>AB; OA+OD>AD ; OB+OC>CD ; OC+OC>CD
Cộng từng vế lại ta được 2AC+2BD>AB+BC+CD+DA(dpcm)
ủng hộ mik nhá ;)