K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
9 tháng 9 2017
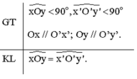
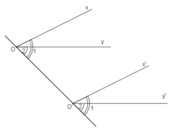
Chứng minh:
Vẽ đường thẳng OO’
Vì Ox // O’x’ nên hai góc đồng vị ∠(O1) và ∠(O'1) bằng nhau
Suy ra: ∠(O1) = ∠(O'1 ) (1)
Vì Oy // O’y’ nên hai góc đồng vị ∠(O2) và ∠(O'2) bằng nhau
Suy ra: ∠(O2) = ∠(O'2)(2)
Từ (1) và (2) suy ra: ∠(O1) - ∠(O2) =∠(O'1) - ∠(O'2)
Vậy ∠(xOy) = ∠(x'O'y')

10 tháng 9 2020
Đặt H là giao điểm của Oy và O'x'
Vì Ox//O'x'
=>O1ˆO1^=H1ˆH1^( đồng vị)
Vì Oy//O'y'
=>H1ˆH1^=O′1ˆO1′^( đồng vị)
Do đó:O1ˆO1^=O′1ˆO1′^
VậyxOyˆ=x′O′y′ˆxOy^=x′O′y′^
Vì Ox // O'x' nên \(\widehat{O_1}=\widehat{O'_1}\) (2 góc đồng vị) (1)
Vì Oy // O'y' nên \(\widehat{O_2}=\widehat{O'_2}\) (2 góc đồng vị) (2)
Từ (1) và (2) suy ra:
\(\widehat{O_1}-\widehat{O_2}=\widehat{O'_1}-\widehat{O'_2}\)
hay \(\widehat{xOy}=\widehat{x'O'y'}\).