Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là chữ số hàng chục \(\left(x\in N,0< x\le9\right)\)
Gọi y là chữ số hàng đơn vị \(\left(y\in N,0\le y\le9\right)\)
Số ban đầu là: \(\overline{xy}=10x+y\)
Số lúc sau: \(\overline{xyx}=100x+10y+x=101x+10y\)
Do chữ số hàng chục lớn hơn chữ số hàng đơn vị là 2 nên: x - y = 2
Do số mới lớn hơn số ban đầu 682 nên: \(101x+10y-10x-y=682\)
\(\Leftrightarrow91x+9y=682\)
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}x-y=2\\91x+9y=682\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}91x-91y=182\\91x+9y=682\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-100y=-500\\x-y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=5\\x=7\end{matrix}\right.\)
Vậy số cần tìm là 75

Gọi chữ số hàng chục của số cần tìm là a, chữ số hàng đơn vị của số cần tìm là b (a thuộc N*, b thuộc n)
Khi đó, số cần tìm có dạng: 10a+b
Nếu viết thêm chữ số hạng chục vào bên phải số cần tìm thì khi đó số mới có dạng: 100a+ 10b+a=101a+10b
Mà số mới này hơn số đã cho 682 đơn vị
=>101a+10b-10a-b=682
<=>91a+9b=682 (1)
Theo đề ta có: a-b=2 <=>b=a-2(2)
Thay (2) vào (1) ta được:
91a+9 (a-2)=682
<=>100a=700
<=>a=7(thỏa điều kiện)
=> b=a-2=7-2=5 (thỏa điều kiện)
Vậy,số đã cho là 75

Gọi số cần tìm là ab .Theo đề bài ta có b= a-2
aba - ab = 682
101a+10b-10a-b=682
91a+9b=682
91a+9(a-2)=682
100a=682+18
100a=700
a=7 => b=5
Vậy số cần tìm là 75

Gọi số cần tìm là \(\overline{ab}\)(Điều kiện: \(\left\{{}\begin{matrix}a,b\in N\\0< a\le10\\0\le b\le10\end{matrix}\right.\))
Vì ba lần chữ số hàng chục lớn hơn chữ số hàng đơn vị là 6 đơn vị nên ta có phương trình: \(3a-b=6\)(1)
Vì khi viết hai chữ số ấy theo thứ tự ngược lại thì được một số mới lớn hơn số cũ là 36 đơn vị nên ta có phương trình: \(10b+a-\left(10a+b\right)=36\)
\(\Leftrightarrow10b+a-10a-b=36\)
\(\Leftrightarrow-9a+9b=36\)
\(\Leftrightarrow a-b=-4\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}3a-b=6\\a-b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=10\\a-b=-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=5\\b=a+4=5+4=9\end{matrix}\right.\)(thỏa ĐK)
Vậy: Số cần tìm là 59

Gọi số cần tìm là \(\overline{ab}\left(ĐK:0\le a,b\le9,a\ne0\right)\)
Theo bài ra, ta có: \(3a+2b=22\left(1\right)\) và \(\frac{\overline{ba}}{\overline{ab}}=\frac{6}{5}\left(2\right)\)
Từ (2) ta có: \(5\left(10b+a\right)=6\left(10a+b\right)\Leftrightarrow44b=55a\Leftrightarrow4b=5a\Leftrightarrow b=\frac{5}{4}a\left(3\right)\)
Thay (3) vào (1) ta có: \(3a+\frac{5}{2}a=22\Leftrightarrow a=4\Rightarrow b=5\Rightarrow\overline{ab}=45\left(tm\right)\)

Gọi x là chữ số hàng chục, y là chữ số hàng đơn vị.
Điều kiện: x, y ∈N*, 0 < x ≤ 9; 0 < y ≤ 9
Vì hai lần chữ số hàng chục lớn hơn 5 lần chữ số hàng đơn vị là 1 nên ta có: 2x – 5y = 1
Vì chữ số hàng chục chia cho chữ số hàng đơn vị được thương là 2 và dư cũng là 2 nên ta có: x = 2y + 2
Ta có hệ phương trình:
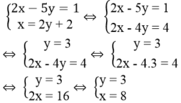
Giá trị của x và y thỏa mãn điều kiện bài toán.
Vậy số cần tìm là 83.

Gọi số cần tìm là \(\overline{xy}\)
+) Do hiệu của 3 lần chữ số hàng chục với 2 lần chữ số hàng đơn vị là 11 nên ta có phương trình \(3x-2y=11\left(1\right)\)
+) Lại có, nếu đổi chữ số hàng chục và hàng đơn vị cho nhau, ta sẽ được 1 số mới nhỏ hơn số cũ 18 đơn vị, hay
\(\overline{xy}-\overline{yx}=18\Leftrightarrow\left(10x+y\right)-\left(10y+x\right)=18\Leftrightarrow9x-9y=18\Leftrightarrow x-y=2\left(2\right)\)
Từ (1) và (2), ta có hệ phương trình:
\(\left\{{}\begin{matrix}3x-2y=11\\x-y=2\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}3x-2y=11\\2x-2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=5\end{matrix}\right.\)
Vậy số cần tìm là 75
Gọi số cần tìm là \(\overline{ab}\) (0<a<10; 0<b<10) => 3a - 2b = 11 (1)
Khi đổi chỗ hai chữ số cho nhau được số mới là \(\overline{ba}\)
Do số mới nhỏ hơn số cũ 18 đơn vị => \(\overline{ab}\) - \(\overline{ba}\) = 18
⇔ 10a + b - 10b - a = 18
⇔ 9a - 9b = 18 (2)
Từ (1) và (2) ta có hệ phương trình:\(\left\{{}\begin{matrix}3a-2b=11\\9a-9b=18\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}9a-6b=33\\9a-9b=18\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}-3b=-15\\9a-9b=18\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}a=7\\b=5\end{matrix}\right.\) (tm)
Vậy số cần tìm là 75

Gọi chữ số hàng chục là : x ; chữ số hàng đơn vị là : y . Trong đó { \(x,y\in N\); \(x\ne0\)}
Số đó có dạng : \(\overline{xy}\)
Vì chữ số hàng chục lớn hơn chữ số hàng đơn vị là 2 , nên ta có phương trình :
x - y = 2 (1)
Vì nếu lấy số đó chia cho tổng các chữ số của nó thì được thương là 6 dư 2 nên :
\(\overline{xy}=\left(x+y\right).6+1\)
\(\Leftrightarrow10.x+y=6x+6y+1\)
\(\Leftrightarrow4x-5y=1\)(2)
Từ (1) và (2) ta được hệ phương trình :
\(\hept{\begin{cases}x-y=2\\4x-5y=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}4x-4y=8\\4x-5y=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=7\\4x-5.7=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=7\\x=9\end{cases}}\)
Vậy số cần tìm là : 97
do tận cùng 6 nên ta tách số chính phương đó thành A6 với A là số tự nhiên muốn bao nhiêu cx dc ta có (A6)2 = 100A2 +120A +36
chữ số hàng chục sẽ là 2A+3 100% là lẻ đấy