K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TM
4
AH
Akai Haruma
Giáo viên
23 tháng 1 2022
Lời giải:
Bổ sung điều kiện $a,b$ là các số dương. Áp dụng BĐT Cô-si ta có:
$a+b\geq 2\sqrt{ab}$
$\frac{1}{a}+\frac{1}{b}\geq 2\sqrt{\frac{1}{ab}}$
$\Rightarrow (a+b)(\frac{1}{a}+\frac{1}{b})\geq 2\sqrt{ab}.2\sqrt{\frac{1}{ab}}=4$
Ta có đpcm
Dấu "=" xảy ra khi $a=b$
TT
1
4 tháng 11 2017
Ta có :
<=> u3 - 3u - 2 \(\le\) v3 - 3v + 2 <=> ( u + 1 )2( u - 2 ) \(\le\) ( v - 1 )2( v + 2 )
Đặt x = u + 1 , y = v -1 thì :
BĐT <=> x3 - 3x2 \(\le\) y3 + 3y2 <=> x3 - y3 \(\le\) 3(x2 + y2)
Ta có : x - y = ( u - v ) + 2 \(\le\)2
=> ( x - y ) ( x2 + xy + y2 ) \(\le\)2( x2 + xy + y2) = 2(x2 + y2) + 2xy \(\le\) 2(x2 + y2) + ( x2 + y2 ) = 3(x2 + y2 ) => x3 - y3 \(\le\) 3(x2 +y2 ) ( đpcm)
Dấu bằng xảy ra khi <=> x = y = 0 <=> u = -1 ; v = 1
DT
0
DT
0
22 tháng 1 2022
Coi như a, b, c là số dương
Áp dụng BĐT Cô-si ta có:
\(\dfrac{a}{bc}+\dfrac{c}{ba}\ge2\sqrt{\dfrac{a}{bc}.\dfrac{c}{ba}}=2\sqrt{\dfrac{1}{b^2}}=\dfrac{2}{b}\left(1\right)\)
Dấu "=" xảy ra ...
\(\dfrac{a}{bc}+\dfrac{b}{ac}\ge2\sqrt{\dfrac{a}{bc}.\dfrac{b}{ac}}=2\sqrt{\dfrac{1}{c^2}}=\dfrac{2}{c}\left(2\right)\)
Dấu "=" xảy ra ...
\(\dfrac{c}{ba}+\dfrac{b}{ac}\ge2\sqrt{\dfrac{c}{ba}+\dfrac{b}{ac}}=2\sqrt{\dfrac{1}{a^2}}=\dfrac{2}{a}\left(3\right)\)
Dấu "=" xảy ra ...
Từ (1), (2), (3) ta có:
\(\dfrac{a}{bc}+\dfrac{c}{ba}+\dfrac{a}{bc}+\dfrac{b}{ac}+\dfrac{c}{ba}+\dfrac{b}{ac}\ge\dfrac{2}{a}+\dfrac{2}{b}+\dfrac{2}{c}\\ \Rightarrow2\left(\dfrac{a}{bc}+\dfrac{b}{ac}+\dfrac{c}{ba}\right)\ge2\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\\ \Rightarrow\dfrac{a}{bc}+\dfrac{b}{ac}+\dfrac{c}{ba}\ge\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)
Dấu "=" xảy ra ...
Vậy ...
12 tháng 1 2021
3 < 4
⇒ 3 < 22 (1)
1 < 2
⇒ 1 < \(\sqrt{2}\)
⇒ 2 < 1 + \(\sqrt{2}\)
⇒ 22 < 21 +\(\sqrt{2}\) (2)
Từ (1), (2) => Đpcm
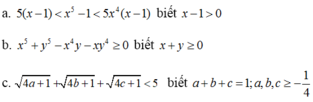
a) Ta có: x5 – 1 = (x – 1)(x4 + x3 + x2 + x + 1)
Lại có: x – 1 > 0 ⇒ x > 1 ⇒ x5 > x4 > x3 > x2 > x > 1
⇒ 1 + 1 + 1 + 1 + 1 < x4 + x3 + x2 + x + 1 < x4 + x4 + x4 + x4 + x4
hay 5 < x4 + x3 + x2 + x + 1 < 5x4
⇒ 5.(x – 1) < (x – 1)(x4 + x3 + x2 + x + 1) < 5x4.(x – 1)
hay 5.(x – 1) < x5 – 1 < 5x4.(x – 1) (đpcm)
b) x5 + y5 – x4y – xy4 = (x5 - x4y) - (xy4 - y5)
= x4.(x – y) – y4.(x – y)
= (x4 – y4).(x – y)
= (x2 + y2)(x2 – y2)(x – y)
= (x2 + y2).(x + y)(x – y)(x – y)
= (x2 + y2)(x + y)(x – y)2
Mà x2 + y2 ≥ 0; x + y ≥ 0; (x – y)2 ≥ 0
⇒ x5 + y5 – x4y – xy4 ≥ 0.
c) Ta có: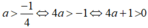
Tương tự. 4b +1 >0 và 4c +1 > 0
Áp dụng bất đẳng thức Cô-si cho hai số dương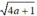
và 1 ta có:
Không có giá trị nào của a, b, c thỏa mãn hệ trên nên dấu “=” của BĐT không xảy ra.