Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi ƯCLN(n+3,2n+5) = d
=> n+3 chia hết cho d, 2n+5 chia hết cho d
=> 2(n+3) chia hết cho d, 2n+5 chia hết cho d
=> 2n+6 chia hết cho d,2n+5 chia hết cho d
=> (2n+6)-(2n+5) chia hết cho d
=> 1 chia hết cho d =>đpcm.

Gọi \(d\inƯ\left(n+15;n+72\right)\) ( \(d\in N,d\ne0\))
\(\Rightarrow n+15⋮d\)
\(n+72⋮d\)
\(\Rightarrow\left(n+72\right)-\left(n+15\right)⋮d\)
\(\Rightarrow57⋮d\)
\(\Rightarrow d=1;3;19;57\) để n + 15 và n + 72 là hai số nguyên tố cùng nhau thì n khác dạng 19k + 15
Vậy có vô số giá trị n

Gọi d \(\in\) ƯC( 2n + 5;n + 2)
\(\text{⇒2n+5−2(n+2)}\) chia hết cho dd
hay 1chia hết cho d
\(\text{⇒d=1}\)
vậy 2n+5 và n+2 nguyên tố cùng nhau
Gọi d ∈∈ ƯC( 2n + 5;n + 2)
⇒2n+5−2(n+2)⇒2n+5−2(n+2) chia hết cho dd
hay 1chia hết cho d
⇒d=1⇒d=1
vậy 2n+5 và n+2 nguyên tố cùng nhau

gọi d\(\in\)ƯC(5n+7;7n+10) thì \(\text{5(7n+10)−7(5n+7)}\) chia hết cho dd
\(\Rightarrow\)1 chia hết cho d
\(\Rightarrow\)d = 1
do đó 7n+10 và 5n+7 nguyên tố cùng nhau
gọi d∈∈ƯC(5n+7;7n+10) thì 5(7n+10)−7(5n+7)5(7n+10)−7(5n+7) chia hết cho dd
⇒⇒1 chia hết cho d
⇒⇒d = 1
do đó 7n+10 và 5n+7 nguyên tố cùng nhau

Câu 1 : Việc gõ ký hiệu như bạn đề cập ; mình cũng không biết phải làm sao nên cứ dùng xyz vậy thôi.
Ta có:
xyz = 100x +10y +z = 111x -11x +10y +z = 37.3x -(11x-10y-z) chia hết cho 37
=> (11x-10y-z) chia hết cho 37
Lại có:
xyz -yzx = 100x +10y +z -100y -10z -x = 99x -90y -9z = 9.(11x-10y-z) chia hết cho 37
Vậy yzx cũng phải chia hết cho 37
Có thể phát biểu hay hơn là CMR: Khi hoán vị các chữ số của 1 số có 3 chữ số chia hết cho 37 thì được số mới cũng chia hết cho 37.

Gọi d\(\in\) ÚC(7n+10, 5n+7) thì 5(7n+10) - 7(5n+7) chia hết cho dd
\(\Rightarrow\) 1 chia hết cho d
\(\Rightarrow\)d=1
Váy 7n+10 và 5n+7 là hai số nguyên tố cùng nhau
Gọi d>0 là ước số chung của 7n+10 và 5n+7
=>d là ước của số 5.(7n+10)= 35n+50
và d là ước của số 7.(5n+7)=35n+49
mà (35n+50)-(35n+49)=1
=> d là ước của số 1=>d=1
Vậy d là ước của 1

Đáp án A.
Cách 1:
∫ 1 2 2 d x x 3 + 3 x 2 + 2 x = 2. ∫ 1 2 1 x x + 1 x + 2 d x = 2 3 . ∫ 1 2 1 x x + 2 + 1 x x + 1 − 2 x + 1 x + 2 d x
= 2 3 ∫ 1 2 1 2 x − 1 2 x + 4 + 1 x − 1 x + 1 − 2 x + 1 + 2 x + 2 d x
∲ = 2 3 ∫ 1 2 3 2 . 1 x − 3 x + 1 + 3 2 . 1 x + 2 d x = ∫ 1 2 1 x d x − 2. ∫ 1 2 1 x + 1 d x + ∫ 1 2 1 x + 2 d x
= ln x 1 2 − 2. ln x + 1 1 2 + ln x + 2 1 2 = ln 2 − ln 1 − 2. ln 3 − ln 2 + ln 4 − ln 3 = ln 32 27
⇒ a = 32 ; b = 27 ⇒ a + b = 59
Cách 2: Sử dụng máy tính.

Lúc này ∫ 1 2 2 d x x 3 + 3 x 2 + 2 x = A n s .
Suy ra a b = e A n s
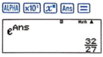
⇒ a b = 32 27 ⇒ a + b = 59
Gọi 2 số tự nhiên liên tiếp là n và n+1
Gọi d là UCLN (n , n+1 ) [ d thuộc N* ]
Ta có n : d => [( n +1 )-n ] : d
n+1 : d
=> 1 : d => d = 1
UCLN ( n , n + 1 ) =1
vậy 2 số tự nhiên liên tiếp là 2 số nguyên tố cùng nhau
tich nha
Gọi số thứ nhất là n, số thứ hai là n+1, ƯC﴾n,n+1﴿=a
Ta có: n chia hết cho a﴾1﴿
n+1 chia hết cho a﴾2﴿
Từ ﴾1﴿ và ﴾2﴿ ta được: n+1‐n chia hết cho a
=> 1 chia hết cho a
=> a=1
=> ƯC﴾n,n+1﴿=1
=> n và n+1 là hai số nguyên tố cùng nhau.
Vậy 2 số tự nhiên liên tiếp là hai số nguyên tố cùng nhau