Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\dfrac{tan2\alpha}{tan4\alpha-tan2\alpha}=\dfrac{sin2\alpha}{cos2\alpha}:\left(\dfrac{sin4\alpha}{cos4\alpha}-\dfrac{sin2\alpha}{cos2\alpha}\right)\)
\(=\dfrac{sin2\alpha}{cos2\alpha}:\dfrac{sin4\alpha cos2\alpha-sin2\alpha cos4\alpha}{cos4\alpha cos2\alpha}\)
\(=\dfrac{sin2\alpha}{cos2\alpha}.\dfrac{cos4\alpha.cos2\alpha}{sin2\alpha}=cos4\alpha\).
b) \(\sqrt{1+sin\alpha}-\sqrt{1-sin\alpha}=\sqrt{sin^2\dfrac{\alpha}{2}+2sin\dfrac{\alpha}{2}cos\dfrac{\alpha}{2}+cos^2\dfrac{\alpha}{2}}\)\(-\sqrt{sin^2\dfrac{\alpha}{2}-2sin\dfrac{\alpha}{2}cos\dfrac{\alpha}{2}+cos^2\dfrac{\alpha}{2}}\)
\(=\sqrt{\left(sin\dfrac{\alpha}{2}+cos\dfrac{\alpha}{2}\right)^2}-\sqrt{\left(sin\dfrac{\alpha}{2}-cos\dfrac{\alpha}{2}\right)^2}\)
\(=\left|sin\dfrac{\alpha}{2}+cos\dfrac{\alpha}{2}\right|-\left|sin\dfrac{\alpha}{2}-cos\dfrac{\alpha}{2}\right|\)
Vì \(0< \alpha< \dfrac{\pi}{2}\) nên \(0< \alpha< \dfrac{\pi}{4}\).
Trong \(\left(0;\dfrac{\pi}{4}\right)\) thì \(sin\dfrac{\alpha}{2}\) tăng dần từ 0 tới \(\dfrac{\sqrt{2}}{2}\) và \(cos\dfrac{\alpha}{2}\) giảm dần từ 1 tới \(\dfrac{\sqrt{2}}{2}\) nên \(\left|sin\dfrac{\alpha}{4}-cos\dfrac{\alpha}{4}\right|=-\left(sin\dfrac{\alpha}{4}-cos\dfrac{\alpha}{4}\right)=cos\dfrac{\alpha}{4}-sin\dfrac{\alpha}{4}\).
Vì vậy:
\(\left|sin\dfrac{\alpha}{2}+cos\dfrac{\alpha}{2}\right|-\left|sin\dfrac{\alpha}{2}-cos\dfrac{\alpha}{2}\right|\)
\(=sin\dfrac{\alpha}{4}+cos\dfrac{\alpha}{4}-\left(cos\dfrac{\alpha}{4}-sin\dfrac{\alpha}{4}\right)=2sin\dfrac{\alpha}{4}\).

\(\dfrac{sina+sin5a+sin3a}{cosa+cos5a+cos3a}=\dfrac{2sin3a.cos2a+sin3a}{2cos3a.cos2a+cos3a}=\dfrac{sin3a\left(2cos2a+1\right)}{cos3a\left(2cos2a+1\right)}=\dfrac{sin3a}{cos3a}=tan3a\)
\(\dfrac{1+sin4a-cos4a}{1+sin4a+cos4a}=\dfrac{1+2sin2a.cos2a-\left(1-2sin^22a\right)}{1+2sin2a.cos2a+2cos^22a-1}=\dfrac{2sin2a\left(sin2a+cos2a\right)}{2cos2a\left(sin2a+cos2a\right)}=\dfrac{sin2a}{cos2a}=tan2a\)
\(96\sqrt{3}sin\left(\dfrac{\pi}{48}\right)cos\left(\dfrac{\pi}{48}\right)cos\left(\dfrac{\pi}{24}\right)cos\left(\dfrac{\pi}{12}\right)cos\left(\dfrac{\pi}{6}\right)=48\sqrt{3}sin\left(\dfrac{\pi}{24}\right)cos\left(\dfrac{\pi}{24}\right)cos\left(\dfrac{\pi}{12}\right)cos\left(\dfrac{\pi}{6}\right)\)
\(=24\sqrt{3}sin\left(\dfrac{\pi}{12}\right)cos\left(\dfrac{\pi}{12}\right)cos\left(\dfrac{\pi}{6}\right)=12\sqrt{3}sin\left(\dfrac{\pi}{6}\right)cos\left(\dfrac{\pi}{6}\right)\)
\(=6\sqrt{3}sin\left(\dfrac{\pi}{3}\right)=6\sqrt{3}.\dfrac{\sqrt{3}}{2}=9\)
\(A+B+C=\pi\Rightarrow A+B=\pi-C\Rightarrow tan\left(A+B\right)=tan\left(\pi-C\right)\)
\(\Rightarrow\dfrac{tanA+tanB}{1-tanA.tanB}=-tanC\Rightarrow tanA+tanB=-tanC+tanA.tanB.tanC\)
\(\Rightarrow tanA+tanB+tanC=tanA.tanB.tanC\)

a) \(tan3\alpha-tan2\alpha-tan\alpha=\left(tan3\alpha-tan\alpha\right)-tan2\alpha\)
\(=\left(\dfrac{sin3\alpha}{cos3\alpha}-\dfrac{sin\alpha}{cos\alpha}\right)-\dfrac{sin2\alpha}{cos2\alpha}\)\(=\dfrac{sin3\alpha cos\alpha-cos3\alpha sin\alpha}{cos3\alpha cos\alpha}-\dfrac{sin2\alpha}{cos2\alpha}\)
\(=\dfrac{sin2\alpha}{cos3\alpha cos\alpha}-\dfrac{sin2\alpha}{cos2\alpha}\)
\(=sin2\alpha.\left(\dfrac{1}{cos3\alpha cos\alpha}-\dfrac{1}{cos2\alpha}\right)\)
\(=sin2\alpha.\dfrac{cos2\alpha-cos3\alpha cos\alpha}{cos3\alpha cos\alpha cos2\alpha}\)
\(=sin2\alpha.\dfrac{cos2\alpha-\dfrac{1}{2}\left(cos4\alpha+cos2\alpha\right)}{cos3\alpha cos2\alpha cos\alpha}\)
\(=sin2\alpha.\dfrac{cos2\alpha-cos4\alpha}{2cos3\alpha cos2\alpha cos\alpha}\)
\(=\dfrac{sin2\alpha.2sin3\alpha.sin\alpha}{2cos3\alpha cos2\alpha cos\alpha}\)
\(=tan3\alpha tan2\alpha tan\alpha\) (Đpcm).
b) \(\dfrac{4tan\alpha\left(1-tan^2\alpha\right)}{\left(1+tan^2\right)^2}=4tan\alpha\left(1-tan^2\alpha\right):\left(\dfrac{1}{cos^2\alpha}\right)^2\)
\(=4tan\alpha\left(1-tan^2\alpha\right)cos^4\alpha\)
\(=4\dfrac{sin\alpha}{cos\alpha}\left(1-\dfrac{sin^2\alpha}{cos^2\alpha}\right)cos^4\alpha\)
\(=4sin\alpha\left(cos^2\alpha-sin^2\alpha\right)cos\alpha\)
\(=4sin\alpha cos\alpha.cos2\alpha\)
\(=2.sin2\alpha.cos2\alpha=sin4\alpha\) (Đpcm).

\(\frac{sin^2a-cos^2a}{1+2sina.cosa}=\frac{\left(sina-cosa\right)\left(sina+cosa\right)}{sin^2a+cos^2a+2sina.cosa}=\frac{\left(sina-cosa\right)\left(sina+cosa\right)}{\left(sina+cosa\right)^2}\)
\(=\frac{sina-cosa}{sina+cosa}=\frac{\frac{sina}{cosa}-\frac{cosa}{cosa}}{\frac{sina}{cosa}+\frac{cosa}{cosa}}=\frac{tana-1}{tana+1}\)

\(\frac{1-cosa+cos2a}{sin2a-sina}=\frac{1-cosa+2cos^2a-1}{2sina.cosa-sina}=\frac{cosa\left(2cosa-1\right)}{sina\left(2cosa-1\right)}=\frac{cosa}{sina}=cota\)

a) \(A=2\left(sin^6\alpha+cos^6\alpha\right)-3\left(sin^4\alpha+cos^4\alpha\right)\)
\(=2\left(sin^2\alpha+cos^2\alpha\right)\left(sin^4\alpha-sin^2\alpha cos^2\alpha+cos^4\alpha\right)\)\(-3\left(sin^4\alpha+cos^4\alpha\right)\)
\(=2\left(sin^4\alpha+cos^4\alpha-sin^2\alpha cos^2\alpha\right)-3\left(sin^4\alpha+cos^4\alpha\right)\)
\(=-\left(sin^4\alpha+cos^4\alpha+2sin^2\alpha cos^2\alpha\right)\)
\(=-\left(sin^2\alpha+cos^2\alpha\right)^2=-1\) (Không phụ thuộc vào \(\alpha\)).
b) \(B=4\left(sin^4\alpha+cos^4\alpha\right)-cos4\alpha\)
\(=4\left(sin^4\alpha+cos^4\alpha+2sin^2\alpha cos^2\alpha\right)-8sin^2\alpha cos^2\alpha\)\(-\left(1-2sin^22\alpha\right)\)
\(=4.\left(sin^2\alpha+cos^2\alpha\right)^2-2sin^22\alpha-1+2sin^22\alpha\)
\(=4-1=3\).

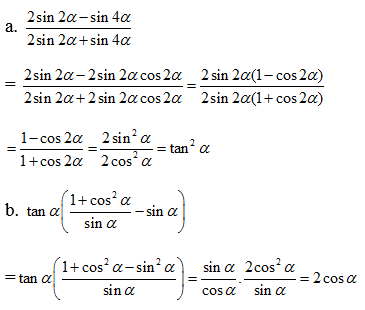
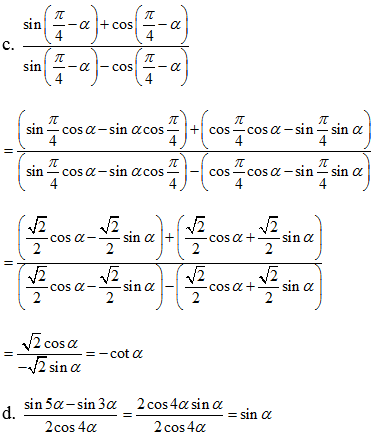
\(VT=\frac{2\cos2\alpha.\cos\alpha}{2.\sin2\alpha\cos\alpha}.\frac{\sin2\alpha}{\cos2\alpha}-2\left(2\sin\alpha.\cos\alpha\right)^2\)
\(VT=1-2\left(\sin2\alpha\right)^2=\cos4\alpha\)