K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

AH
Akai Haruma
Giáo viên
8 tháng 3 2021
Bài 1:
Áp dụng BĐT Bunhiacopxky ta có:
$(a^2+b^2+c^2)(1+1+1)\geq (a+b+c)^2$
$\Leftrightarrow 3(a^2+b^2+c^2)\geq 1$
$\Leftrightarrow a^2+b^2+c^2\geq \frac{1}{3}$ (đpcm)
Dấu "=" xảy ra khi $a=b=c=\frac{1}{3}$
AH
Akai Haruma
Giáo viên
8 tháng 3 2021
Bài 2:
Áp dụng BĐT Bunhiacopxky:
$(a^2+4b^2+9c^2)(1+\frac{1}{4}+\frac{1}{9})\geq (a+b+c)^2$
$\Leftrightarrow 2015.\frac{49}{36}\geq (a+b+c)^2$
$\Leftrightarrow \frac{98735}{36}\geq (a+b+c)^2$
$\Rightarrow a+b+c\leq \frac{7\sqrt{2015}}{6}$ chứ không phải $\frac{\sqrt{14}}{6}$ :''>>

CM
20 tháng 6 2017
Chọn C.
Phương án A : biểu thức tọa độ tích vô hướng nên loại A.
Phương án B : Công thức tích vô hướng của hai véc tơ ![]() nên loại B.
nên loại B.
Phương án C: 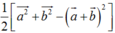
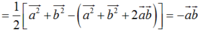 nên chọn C.
nên chọn C.
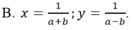
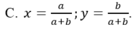
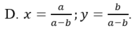
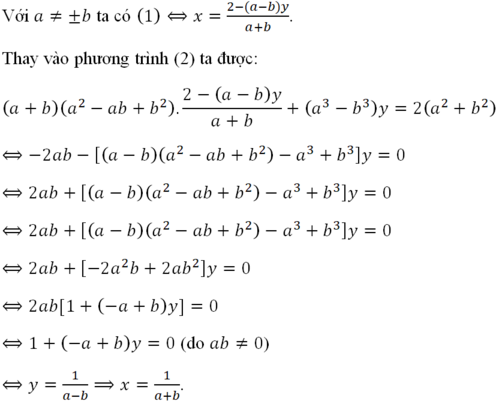


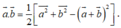
chữ " b" mk ghi ở phần b) trước "CMR " là gõ nhầm đấy, ko liên quan j đến bài toán đâu !!