Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Gọi x, y, z theo thứ tự tăng dần của độ dài ba cạnh của tam giác.
Chu vi của tam giác: x + y + z = 3a (1)
Tính chất của cấp số cộng có x + z = 2y (2)
Vì tam giác vuông nên có: x2 + y2 = z2 (3)
Thay (2) vào (1) được 3y = 3a hay y = a, thay y = a vào (2) được: x + z = 2a hay x = 2a - z
Thay x và y vào (3) được: (2a – z)2 + a2 = z2 ⇔ 5a2 – 4az = 0 ⇔ 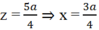
Độ dài ba cạnh của tam giác thỏa yêu cầu: 
Vậy độ dài cạnh lớn nhất của tam giác là ![]()

Chọn C
Ba cạnh a, b, c ( a < b < c) của một tam giác theo thứ tự đó lập thành một cấp số cộng thỏa mãn yêu cầu thì:
a 2 + b 2 = c 2 a + b + c = 3 a + c = 2 b ⇔ a 2 + b 2 = c 2 3 b = 3 a + c = 2 b ⇔ a 2 + b 2 = c 2 b = 1 a = 2 b − c = 2 − c .
Ta có
a 2 + b 2 = c 2 → a = 2 − c b = 1 2 − c 2 + 1 = c 2
⇔ − 4 c + 5 = 0 ⇔ c = 5 4 ⇒ a = 3 4 b = 1 c = 5 4 .

Gọi 3 cạnh tam giác là \(a\) ; \(a+d\) ; \(a+2d\) (với \(a>d\))
\(p=\dfrac{3a+3d}{2}\) ; \(r^2=\dfrac{\left(p-a\right)\left(p-b\right)\left(p-c\right)}{p}=9\)
\(\Rightarrow\left(\dfrac{a+3d}{2}\right)\left(\dfrac{a+d}{2}\right)\left(\dfrac{a-d}{2}\right)=\dfrac{27}{2}\left(a+d\right)\)
\(\Leftrightarrow\left(a+3d\right)\left(a-d\right)=108\)
Do \(\left(a+3d\right)+\left(a-d\right)=2\left(a+d\right)\) chẵn ta chỉ cần xét các cặp ước dương cùng tính chẵn lẻ của 108
TH1: \(\left\{{}\begin{matrix}a+3d=54\\a-d=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=15\\d=13\end{matrix}\right.\)
Ba cạnh là: \(\left(15;28;41\right)\)
TH2: \(\left\{{}\begin{matrix}a+3d=18\\a-d=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=9\\d=3\end{matrix}\right.\)
Ba cạnh là: \(\left(9;12;15\right)\)

Đáp án B.
Các cạnh từ bé đến lơn tạo thành một cấp số cộng có ![]() và công sai
và công sai ![]() .
.
Gọi số cạnh của đa giác là ![]()
![]() Chu vi là
Chu vi là
![]()
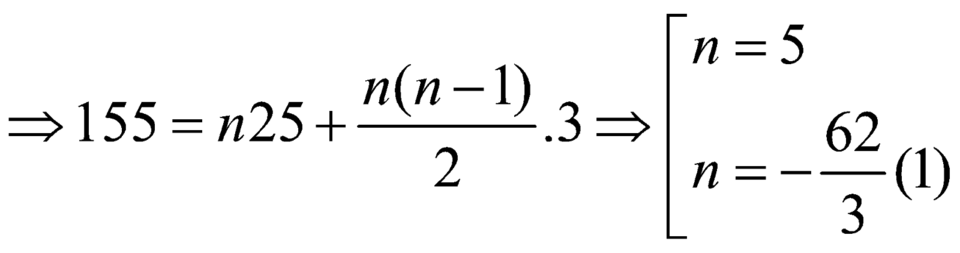
Vậy đa giác đó là ngũ giác.

Gọi số đo ba cạnh của tam giác vuông là x - d, x, x + d
Theo giả thiết ta có x + d 2 = x − d 2 + x 2 (1)
Từ (1) tìm được x = 0, x = 4d
Như vậy có thể có tam giác vuông thoả mãn đầu bài, các cạnh của nó là 3d, 4d, 5d. Đặc biệt, nếu d = 1 thì tam giác vuông có các cạnh là 3, 4, 5 (tam giác Ai Cập).

Gọi số đo ba cạnh của tam giác vuông là \(x-d,x,x+d\)
Theo giả thiết ta có \(\left(x+d\right)^2=\left(x-d\right)^2+x^2\) (1)
Từ (1) tìm được \(x=0;x=4d\)
Như vậy có thể có tam giác vuông thỏa mãn đầu bài, các cạnh của nó là 3d, 4d, 5d. Đặc biệt, nếu \(d=1\) thì tam giác vuông có cách cạnh là 3, 4, 5 (tam giác Ai Cập)
- Gọi độ dài các cạnh của đa giác trên là:\(a_1,a_2,...,a_n\left(cm\right)\left(a_1< a_2< ...< a_n\right)\left(n\in N\cdot,n>2\right)\)
- Vì độ dài các cạnh của đa giác trên lập thành 1 cấp số cộng nên ta có:
\(\left\{{}\begin{matrix}a_n=a_1+\left(n-1\right)d\\a_1+a_2+...+a_n=na_1+\dfrac{n\left(n-1\right)}{2}d\end{matrix}\right.\)
Mặt khác, theo đề bài ta có: \(\left\{{}\begin{matrix}a_n=15\left(cm\right)\\d=3\\a_1+a_2+...+a_n=45\left(cm\right)\end{matrix}\right.\)
Do đó: \(\left\{{}\begin{matrix}a_1+3\left(n-1\right)=15\left(1\right)\\na_1+\dfrac{3n\left(n-1\right)}{2}=45\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Rightarrow na_1+3n\left(n-1\right)=15n\left(3\right)\)
Lấy \(\left(3\right)-\left(2\right)\), ta được: \(\dfrac{3n\left(n-1\right)}{2}=15n-45\)
\(\Leftrightarrow3n^2-3n+90-30n=0\)
\(\Leftrightarrow n^2-11n+30=0\)
\(\Leftrightarrow\left[{}\begin{matrix}n=6\\n=5\end{matrix}\right.\)
*Với \(n=6\). Từ (1) ta có: \(a_1=15-3\left(n-1\right)=15-3\left(6-1\right)=0\) (loại)
*Với \(n=5\). Từ (1) ta có: \(a_1=15-3\left(n-1\right)=15-3\left(5-1\right)=3\left(cm\right)\)
Vậy số cạnh của đa giác đó là 5.