Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu đó là cạnh đáy thì bài toán được chứng minh.
Nếu đó là cạnh bên theo bất đẳng thức tam giác ta có 4x2=8<13(vô lí).
Vậy đó là cạnh đáy.
do tam giác cân nên ta có độ dài 3 cạnh tam giác là: a, a, b
theo đề ta có: 2a+ b= 21
giả sử cạnh đó là cạnh bên---> 2.4+ b= 21<---> b= 21- 8=13---> 2a< b
mà ta lại có: trong 1 tam giác tổng của 2 cạnh luôn luôn lớn hơn cạnh còn lại
----> điều giả sử là vô lý---> cạnh đó là cạnh đáy.

Đáp án B
Ta sắp xếp các cạnh giá trị u 1 ; … u n tăng dần theo cấp số cộng là 3. Khi đó ta có:
S n = 158 u n = 44 ⇔ u 1 + 44 . n 2 = 158 u 1 + 3 n − 1 = 44 ⇔ u 1 = 47 − 3 n 47 − 3 n + 44 . n = 316 *
* ⇔ 3 n 2 − 91 n + 316 = 0 ⇔ n = 4 T M n = 79 3 L

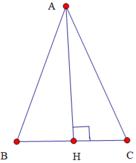
BC và AK cắt BC tại H.Ta có HB=HC (AK là trung trực của BC)
=>HC=BC/2.
AH=√(AC²-CH²);
∆ACH~∆COH (tam giác vuông chung góc nhọn tại O)
=>AH/AC=HC/CO=>CO=AC.HC/AH.
=20.12/√(20²-12²)=20.12/16=15.
Gọi AH, BK là hai đường cao, có AH = 10; BK = 12
thấy hai tgiác CAH và CBK đồng dạng => CA/AH = CB/BK
=> CA/10= 2CH/12 => CA = 2,6.CH (1)
mặt khác áp dụng pitago cho tgiac vuông HAC:
CA² = CH² + AH² (2)
thay (1) vào (2): 2,6².CH² = CH² + 102
=> (2,6² - 1)CH² = 102=> CH = 10 /2,4 = 6,5
=> BC = 2CH = 13 cm


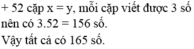


TGọi độ dài cạnh bên là b. Ta có b=(15-a)/2
Do b\(\in\)N => a là số lẻ => a\(\in\)\(\left\{1;3;5;7;9;11;13\right\}\).
Vậy a\(\in\)\(\left\{1;3;5;7;9;11;13\right\}\)
day nha