Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(P\left( A \right)\) là tỉ lệ học sinh học khá môn Ngữ văn trong tổng số học sinh của trường X
\(P\left( B \right)\) là tỉ lệ học sinh học khá môn Toán trong tổng số học sinh của trường X
\(P\left( {AB} \right)\) là tỉ lệ học sinh học khá cả hai môn Ngữ văn và Toán trong tổng số học sinh của trường X
\(P\left( {A \cup B} \right)\) là tỉ lệ học sinh học khá ít nhất một trong hai môn Ngữ văn và Toán trong tổng số học sinh của trường X
b) Ta không áp dụng được công thức \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\) vì hai biến cố A và B không độc lập với nhau do học sinh học khá môn Ngữ Văn có thể cũng học khá môn Toán (7% học sinh học khá cả hai môn Ngữ văn và Toán)

a) A = {Dung, Long, Cường, Trang}
B = {Lan, Hương, Phúc, Cường, Trang}
C = {Dung, Long, Lan, Hương, Phúc, Cường, Trang}
b) A ∪ B = {Dung, Long, Cường, Trang, Lan, Hương, Phúc}
a: A={Dung, Long, Cường, Trang}
B={Lan, Hương, Phúc, Cường, Trang}
C={Dung, Long, Lan, Hương, Phúc, Cường, Trang}
b: A hợp B={Dung,Long,Cường,Trang,Phúc,Hương,Lan}

Ta có n(Ω) = 40
a) Rõ ràng n(A) = 15 nên P(A) = 15/40 = 3/8
Chọn đáp án là C

Ta có n(Ω) = 40
b) Rõ ràng n(B) = 10 nên P(B) = 10/40 =1/4
Chọn đáp án B

Ta có n(Ω) = 40
c) Nhận thấy :
![]()
![]()
Mà P(A∪B) = P(A) + P(B) –P(A∩B), A∩B là biến cố:”học sinh được chọn giỏi cả Văn và Toán” nên n(A∩B)=5/40=1/8
![]()
![]()
Chọn đáp án C
Nhận xét:
ở ý a) và b) học sinh có thể nhầm khi quan niệm: chọn 1 học sinh nên n(A) =n(B) =1 ⇒ phương án A; hoặc chọn 1 học sinh trong 5 học sinh giỏi Toán và Văn nên n(A) =n(B) = 5
⇒ P(A) =P(B) =5/40=1/8 (phương án D); hoặc sử dụng nhầm công thức P(A) =(n(Ω))/(n(A))=8/3;P(B)=(n(Ω))/(n(B))=4 (phương án C)
ở ý c), học sinh có thể nhầm khi quan niệm:
![]()
![]()
![]()
Nhưng A ¯ v à B ¯ không phải là hai biến cố độc lập

![]()
Có thể giải ý c) cách khác như sau:
Số học sinh giỏi Văn và Toán gồm: học sinh giỏi Văn, học sinh hioir Toán, học sinh giỏi cả Văn và Toán nên bằng (15 +10) -5 = 20 em. Do đó, số học sinh không giỏi cả Toán và Văn là 40 – 20 = 20 em, nên n(C) = 20
Vì vậy P(C) =(n(C))/(n(Ω))=1/2

Cặp biến cố E và F không xung khắc vì nếu học sinh được chọn thích môn Bóng đá thì cả E và F có thể xảy ra vì có 2 bạn thích cả hai môn Bóng đá và Cầu lông.
Vì có 2 bạn cùng thích bóng đá và cầu lông
nên hai biến cố E và F không xung khắc

a) Không gian mẫu của bài toán này là tập hợp các học sinh trong tổ lớp, nó có 9 phần tử và được ký hiệu là Ω = {Hương, Hồng, Dung, Phương, Sơn, Tùng, Hoàng, Tiến, Hải}.
b) Biến cố H xảy ra khi học sinh được chọn là một bạn nữ, nó là tập hợp các học sinh nữ và được ký hiệu là
H = {Hương, Hồng, Dung, Phương}.
Biến cố K xảy ra khi học sinh được chọn có tên bắt đầu là chữ cái H, được ký hiệu là
K = {Hương, Hồng, Hoàng}.
Biến cố hợp M xảy ra khi học sinh được chọn là một bạn nữ hoặc có tên bắt đầu bằng chữ H, nó là tập hợp các học sinh trong tập H hoặc K (bao gồm cả những học sinh trùng nhau của hai tập này) và được ký hiệu là
M = H ∪ K = {Hương, Hồng, Dung, Phương, Hoàng}.
a: Ω={Hương, Hồng, Dung, Phương, Sơn, Tùng, Hoàng, Tiến, Hải}
n(Ω)=9
b: H={Hương, Hồng, Dung, Phương}
K={Hương, Hồng, Hoàng}
=>M={Hương,Hồng,Dung,Phương,Hoàng}
H là tập con của M và Ω
K là tập con của M và Ω
M là tập con của Ω

Đáp án A
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố“3 học sinh được chọn luôn có học sinh chọn môn Vật lý và học sinh chọn môn Hóa học”.
Số phần tử của biến cố A là
![]()
Vậy xác suất cần tìm là
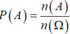
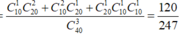
\(P\cup Q\): Học sinh đó hoặc bị cận thị hoặc giỏi môn toán
PQ: Học sinh đó vừa bị cận thị vừa giỏi môn Toán
\(\overline{PQ}\): Học sinh đó vừa không bị cận thị vừa không giỏi môn Toán