Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Sơ đồ tư duy:
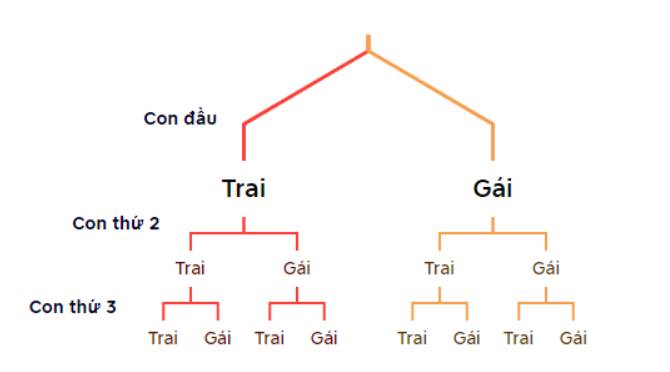
Kí hiệu con trai: T, con gái: G.
Các kết quả có thể xảy ra là: GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT.
Do đó: \(\Omega\)= {GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT}.
Vậy n(Ω) = 8.
b) Gọi biến cố A: “Gia đình đó có một con trai và hai con gái”.
Ta có: A = {GTG; TGG; GGT}. Do đó, \(n(A)\)= 3.
Vậy \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{3}{8}\)

a) Ta có \(\Omega = \left\{ {1;2;...;22} \right\}\).
b) \(B = \left\{ {3;6;9;12;15;18;21} \right\}\).
\(\overline A = \left\{ {1;2;4;5;7;8;10;11;13;14;16;17;19;20;22} \right\}\).

Tổng số khả năng có thể xảy ra của phép thử là \(n\left( \Omega \right) = C_{45}^2.C_{45}^2\)
a) Gọi A là biến cố “Trong 4 bạn được chọn có ít nhất 1 bạn nam”, ta có biến cố đối \(\overline A \): “Trong 4 bạn được chọn không có bạn nam nào”
\(\overline A \) xảy ra khi các bạn được chọn đều là nữ. Số kết quả thuận lợi cho biến cố \(\overline A \) là \(n\left( {\overline A } \right) = C_{20}^2.C_{24}^2\)
Xác suất của biến cố \(\overline A \) là \(P\left( {\overline A } \right) = \frac{{n\left( {\overline A } \right)}}{{n\left( \Omega \right)}} = \frac{{C_{20}^2.C_{24}^2}}{{C_{45}^2.C_{45}^2}} = \frac{{874}}{{16335}}\)
Suy ra, xác suất của biến cố A là \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{874}}{{16335}} = \frac{{15461}}{{16335}}\)
b) Gọi A là biến cố “Trong 4 bạn được chọn có đủ cả nam và nữ” ta có biến cố đối \(\overline A \): “Trong 4 bạn được chọn đều là nữ hoặc đều là nam”
\(\overline A \) xảy ra khi các bạn được chọn đều là nữ hoặc nam. Số kết quả thuận lợi cho biến cố \(\overline A \) là \(n\left( {\overline A } \right) = C_{20}^2.C_{24}^2 + C_{25}^2.C_{21}^2\)
Xác suất của biến cố \(\overline A \) là \(P\left( {\overline A } \right) = \frac{{n\left( {\overline A } \right)}}{{n\left( \Omega \right)}} = \frac{{C_{20}^2.C_{24}^2 + C_{25}^2.C_{21}^2}}{{C_{45}^2.C_{45}^2}} = \frac{{1924}}{{16335}}\)
Suy ra, xác suất của biến cố A là \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{1924}}{{16335}} = \frac{{14411}}{{16335}}\)

Tổng số khả năng có thể xảy ra của phép thử là \(n\left( \Omega \right) = {6^3}\)
a) Gọi A là biến cố “Tổng số chấm xuất hiện nhỏ hơn 5”, ta có biến cố đối của A là \(\overline A \): “Tổng số chấm xuất hiện lớn hơn hoặc bằng 5”
Số kết quả thuận lợi cho \(\overline A \) là \(n\left( {\overline A } \right) = 1 + C_3^1 = 4\)
Xác suất của biến cố \(\overline A \) là \(P\left( {\overline A } \right) = \frac{4}{{{6^3}}} = \frac{1}{{54}}\)
Vậy xác suất của biến cố A là \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{1}{{54}} = \frac{{53}}{{54}}\)
b) Gọi A là biến cố “Tích số chấm xuất hiện chia hết cho 5”, ta có biến cố đối của A là \(\overline A \): “Tích số chấm xuất hiện không chia hết cho 5”
\(\overline A \) xảy ra khi không có mặt của xúc xắc nào xuất hiện 5 chấm
Số kết quả thuận lợi cho \(\overline A \) là \(n\left( {\overline A } \right) = {5^3}\)
Xác suất của biến cố \(\overline A \) là \(P\left( {\overline A } \right) = \frac{{{5^3}}}{{{6^3}}} = \frac{{125}}{{216}}\)
Vậy xác suất của biến cố A là \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{125}}{{216}} = \frac{{91}}{{216}}\)

a) Sơ đồ cây:
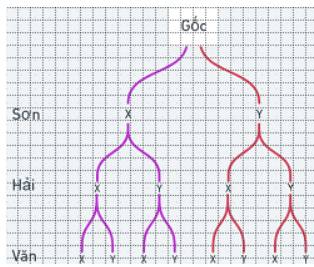
b) Dựa vào sơ đồ cây ta có \(n\left( \Omega \right) = 8\).
Gọi F là biến cố: “Hai bạn vào quán X, bạn còn lại vào quán Y”.
Ta có \(F = \left\{ {XXY;XYX;YXX} \right\}\). Suy ra \(n\left( F \right) = 3\). Vậy \(P\left( F \right) = \frac{3}{8}\).

Chọn ngẫu nhiên 2 người từ 20 người ta được một tổ hợp chập 2 của 20. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{20}^2\)( phần tử)
Gọi A là biến cố “Chọn được 2 người là vợ chồng”
Để chọn được 1 cặp vợ chồng lên khiêu vũ từ 10 cặp vợ chồng ta được một tổ hợp chập 1 của 10 phần tử. Do đó số phần tử của biến cố A là: \(n\left( A \right) = C_{10}^1\)( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{10}^1}}{{C_{20}^2}} = \frac{1}{{19}}\)

a: n(A)=2
n(omega)=2*2*2=8
=>P(A)=2/8=1/4
b: B={(NSS); (SNS); (SSN)}
=>n(B)=3
=>P(B)=3/8
c: C={NSS; NSN; SSN; SSS}
=>n(C)=4
=>P(C)=4/8=1/2
d: D={NSN; NNS; NNN; SNN; NSS; SNS; SSN}
=>n(D)=6
=>P(D)=6/8=3/4

Do các tấm thẻ giống nhau, nên lấy 3 tấm từ 10 tấm không quan tâm thứ tự có \(C_{10}^3 = 120\)cách, suy ra \(n\left( \Omega \right) = 120\)
Gọi A là biến cố “Tích các số ghi trên ba thẻ đó là số chẵn”
Để tích các số trên thẻ là số chẵn thì ít nhất có 1 thẻ là số chẵn
Để chọn ra 3 thẻ thuận lợi cho biến cố A ta có 3 khả năng
+) Khả năng 1: 3 thẻ chọn ra có 1 thẻ có số chẵn và 2 thẻ có số lẻ có \(5.C_5^2 = 50\) khả năng
+) Khả năng 2: 3 thẻ chọn ra có 2 thẻ có số chẵn và 1 thẻ có số lẻ có \(C_5^2.5 = 50\) khả năng
+) Khả năng 3: 3 thẻ chọn ra có đều là có số chắn có \(C_5^3 = 10\) khả năng
Suy ra \(n\left( A \right) = 50 + 50 + 10 = 110\)
Vậy xác suất của biến cố A là: \(P(A) = \frac{{110}}{{120}} = \frac{{11}}{{12}}\)

a) Ta có \(\Omega = \left\{ {1;2;...;30} \right\}\).
b) \(A = \left\{ {2;3;5;7;11;13;17;19;23;29} \right\}\).
\(\overline A = \left\{ {1;4;6;8;9;10;12;14;15;16;18;20;21;22;24;25;26;27;28;30} \right\}\).
Ta có: \(\Omega = \left\{ {TGT;TTG;TTT;TGG;GGT;GTG;GTT;GGG} \right\}\) nên suy ra \(n\left( \Omega \right) = 8\).
a) Ta có \(A = \left\{ {GGT;GTG;GTT;GGG} \right\}\). Suy ra \(n\left( A \right) = 4\).
Từ đó, \(P\left( A \right) = \frac{4}{8} = \frac{1}{2}\).
b) Gọi biến cố \(B\): “Có ít nhất một con trai”.
Ta có \(B = \left\{ {TGT;TTG;TTT;TGG;GGT;GTG;GTT} \right\}\). Suy ra \(n\left( B \right) = 7\).
Từ đó, \(P\left( B \right) = \frac{7}{8}\).