Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Biên độ của dao động là: \(A=10\) (cm)
Tần số góc là: \(\omega=2\pi\) (rad/s)
Tần số là: \(f=\dfrac{\omega}{2\pi}=1\) (Hz)
Chu kì là: \(T=\dfrac{1}{f}=1\) (s)
b. Vận tốc và gia tốc cực đại lần lượt là:
\(v_{max}=\omega A=20\pi\) (cm/s)
\(a_{max}=\omega^2A=400\) (cm/s)
c. Phương trình vận tốc là:
\(v=20\pi\cos\left(2\pi t+\dfrac{\pi}{2}\right)\) (cm/s)

Đáp án B
+ Phát biểu đúng là:
(e) cứ mỗi chu kỳ dao động, có 4 thời điểm thế năng và động năng của vật bằng nhau.
(g) gia tốc đạt giá trị cực tiểu khi vật ở ly độ cực đại.

+ Phát biểu đúng là:
(e) cứ mỗi chu kỳ dao động, có 4 thời điểm thế năng và động năng của vật bằng nhau.
(g) gia tốc đạt giá trị cực tiểu khi vật ở ly độ cực đại.
Đáp án B

Độ lớn của gia tốc không vượt quá 100 c m / s 2 là một phần 3 chu kì → 1 2 ω 2 A = 100 .
→ ω = 2 π rad / s → f = 1 Hz
Đáp án A

Chọn đáp án B
? Lời giải:
+ Với giải thiết bài toán x 1 v 1 + x 2 v 2 = 8 c m 2 / s ⇒ d x 1 x 2 d t = 8 c m 2 / s
Giả sử x 1 = A 1 cos ω t + φ 1 x 2 = A 2 cos ω t + φ 2
⇒ x 1 x 2 = A 1 A 2 cos ω t + φ 1 cos ω t + φ 2 = A 1 A 2 2 cos φ 1 − φ 2 + cos 2 ω t + φ 1 + φ 2
+ Thay vào phương trình đầu ta được ω = 8 − A 1 A 2 sin 2 ω t + φ 1 + φ 2
+ Với A 1 + A 2 2 ≥ A 1 A 2 ⇒ A 1 A 2 ≤ A 1 + A 2 2 2 = 16 c m 2
⇒ ω min khi mẫu số là lớn nhất vậy ω = 8 16 = 0 , 5 r a d / s

Chọn đáp án B
? Lời giải:
+ Với giải thiết bài toán x 1 v 2 + x 2 v 1 = 8 c m 2 / s
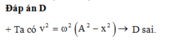
Chọn A.
Giải thích:
Li độ: \(x=Acos\left(\omega t+\varphi\right)\)
Vận tốc: \(v=\omega Acos\left(\omega t+\varphi+\dfrac{\pi}{2}\right)=-\omega Asin\left(\omega t+\varphi\right)\)
Gia tốc: \(a=-\omega^2x=-\omega^2Acos\left(\omega t+\varphi\right)=\omega^2Acos\left(\omega t+\varphi+\pi\right)\)