Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có `xyz=2023=>2023=xyz`
Thay vào ta có :
\(\dfrac{xyz\cdot x}{xy+xyz\cdot x+xyz}+\dfrac{y}{yz+y+xyz}+\dfrac{z}{xz+z+1}=1\\ \dfrac{x^2yz}{xy\left(1+xz+z\right)}+\dfrac{y}{y\left(z+1+xz\right)}+\dfrac{z}{xz+z+1}=1\\ \dfrac{xz}{1+xz+z}+\dfrac{1}{z+1+xz}+\dfrac{z}{xz+z+1}=1\\ \dfrac{xz+1+z}{1+xz+z}=1\left(dpcm\right)\)

a) A = x - y + z + z + y + x - 2y
A = (x + x) + (-y + y) + (z + z) - 2y
A = 2x + 0 + 2z - 2y
A = 2 .(x + z - y)
b) Thay x = 3 ; y = -1 ; z = 2 vào biểu thức A , ta được :
A = 2 .[3 + 2 - (-1)]
A = 12
Vậy A = 12
Chúc bạn học tốt !


mk k ghi đề mà lm luôn nha
Bài 1:
-14 + 13 - 10 = -11
Bài 2: (thay x, y vào)
1) B = - 3 + 7 + (-10) = -3 + 7 - 10 = -6
2) C = -2 - (-5) - (-8) = -2 + 5 + 8 = 11

x=by+cz;y=ax+cz;z=ax+by
=>x+y+z=2(ax+by+cz)
\(\Leftrightarrow\frac{x+y+z}{2}=ax+by+cz\)
\(\Leftrightarrow y+z=\frac{x+y+z}{2}+ax;z+x=\frac{x+y+z}{2}+by;x+y=\frac{x+y+z}{2}+cz\)
\(\Leftrightarrow\frac{y+z-x}{2}=ax;\frac{z+x-y}{2}=by;\frac{x+y-z}{2}=cz\)
\(\Leftrightarrow\frac{y+z-x}{2x}=a;\frac{z+x-y}{2y}=b;\frac{x+y-z}{2z}=c\)
\(\Rightarrow A=\frac{1}{1+\frac{x+y-z}{2z}}+\frac{1}{1+\frac{y+z-x}{2x}}+\frac{1}{1+\frac{z+x-y}{2y}}=\frac{1}{\frac{x+y+z}{2x}}+\frac{1}{\frac{x+y+z}{2y}}+\frac{1}{\frac{x+y+z}{2z}}\)
\(=\frac{2x}{x+y+z}+\frac{2y}{x+y+z}+\frac{2z}{x+y+z}=\frac{2\left(x+y+z\right)}{x+y+z}=2\)
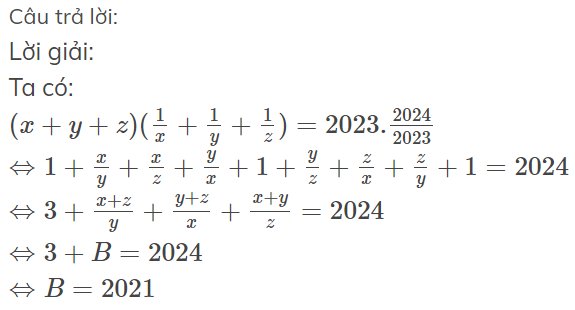
Lời giải:
Ta có:
$(x+y+z)(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})=2023.\frac{2024}{2023}$
$\Leftrightarrow 1+\frac{x}{y}+\frac{x}{z}+\frac{y}{x}+1+\frac{y}{z}+\frac{z}{x}+\frac{z}{y}+1=2024$
$\Leftrightarrow 3+\frac{x+z}{y}+\frac{y+z}{x}+\frac{x+y}{z}=2024$
$\Leftrightarrow 3+B=2024$
$\Leftrightarrow B=2021$