Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TH1: \(x+y+z+t=0\)
\(P=\left(1+\dfrac{x+y}{z+t}\right)^{2023}+\left(1+\dfrac{y+z}{x+t}\right)^{2023}+\left(1+\dfrac{z+t}{x+y}\right)^{2023}+\left(1+\dfrac{t+x}{y+z}\right)^{2023}\)
\(=\left(\dfrac{x+y+z+t}{z+t}\right)^{2023}+\left(\dfrac{x+y+z+t}{x+t}\right)^{2023}+\left(\dfrac{x+y+z+t}{x+y}\right)^{2023}+\left(\dfrac{x+y+z+t}{y+z}\right)^{2023}\)
\(=0+0+0+0=0\) là số nguyên (thỏa mãn)
TH2: \(x+y+z+t\ne0\), áp dụng t/c dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2023x+y+z+t}=\dfrac{y}{x+2023y+z+t}=\dfrac{z}{x+y+2023z+t}+\dfrac{t}{x+y+z+2023t}\)
\(=\dfrac{x+y+z+t}{\left(2023x+y+z+t\right)+\left(x+2023y+z+t\right)+\left(x+y+2023z+t\right)+\left(x+y+z+2023t\right)}\)
\(=\dfrac{x+y+z+t}{2026\left(x+y+z+t\right)}=\dfrac{1}{2026}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{2023x+y+z+t}=\dfrac{1}{2026}\\\dfrac{y}{x+2023y+z+t}=\dfrac{1}{2026}\\\dfrac{z}{x+y+2023z+t}=\dfrac{1}{2026}\\\dfrac{t}{x+y+z+2023t}=\dfrac{1}{2026}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2026x=2023x+y+z+t\\2026y=x+2023y+z+t\\2026z=x+y+2023z+t\\2026t=x+y+z+2023t\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}4x=x+y+z+t\\4y=x+y+z+t\\4z=x+y+z+t\\4t=x+y+z+t\end{matrix}\right.\)
\(\Rightarrow4x=4y=4z=4t\) (vì đều bằng \(x+y+z+t\))
\(\Rightarrow x=y=z=t\)
Do đó:
\(P=\left(1+\dfrac{x+x}{x+x}\right)^{2023}+\left(1+\dfrac{x+x}{x+x}\right)^{2023}+\left(1+\dfrac{x+x}{x+x}\right)^{2023}+\left(1+\dfrac{x+x}{x+x}\right)^{2023}\)
\(=2^{2023}+2^{2023}+2^{2023}+2^{2023}\)
\(=4.2^{2023}=2^{2025}\in Z\)
Em kiểm tra lại đề, 2 ngoặc cuối bị giống nhau, chắc em ghi nhầm

Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{x}{y}=\dfrac{y}{z}=\dfrac{z}{x}=\dfrac{x+y+z}{y+z+x}=\dfrac{x+y+z}{x+y+z}=1\)
\(\Rightarrow\left\{{}\begin{matrix}x=y\\y=z\\z=x\end{matrix}\right.\)
Do đó \(\left\{{}\begin{matrix}x-y=0\\y-z=0\\z-x=0\end{matrix}\right.\)
Thay vào biểu thức \(P=\left(x-y\right)^{2022}+\left(y-z\right)^{2023}+\left(x-z-1\right)^{202}\),ta có:
\(P=0^{2022}+0^{2023}+\left(-1\right)^{202}\)
\(=0+0+1\)
\(=1\)

x-y-z=0
=> x=y+z
y=x-z
-z=y-x
B=(1-z/x)(1-x/y)(1+y/z)
B=((x-z)/x)((y-x)/y)((z+y)/z)
B=(y/x)(-z/y)(x/z)
B=(-z.y.x)/(x.y.z)
B=-1


x - y - z = 0
x = y + z
y = x - z
z = x - y => -z = y - x
B = (1 - z/x)(1 - x/y) (1 + y/z)
B = (x/x - z/x)( y/y - x/y) ( z/z + y/z)
B = \(\frac{x-z}{x}\cdot\frac{y-x}{y}\cdot\frac{z+x}{z}=\frac{y}{x}\cdot\frac{-z}{y}\cdot\frac{x}{z}=-1\)


\(A=\left(1-\frac{z}{x}\right)\left(1-\frac{x}{y}\right)\left(1+\frac{y}{z}\right)=\frac{\left(x-z\right)\left(y-x\right)\left(y+z\right)}{xyz}=\frac{y.\left(-z\right).x}{xyz}=-1\)
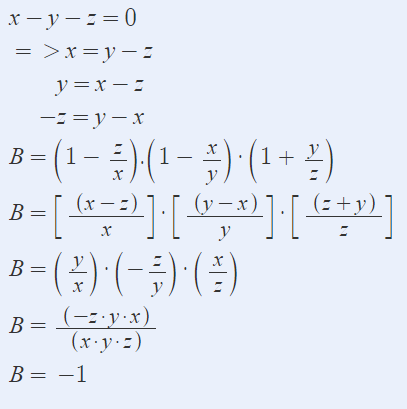
x-y-z=0
=>x=y+z và y=x-z và z=x-y
B=(1-z/x)(1-x/y)(1+y/z)+2023
\(=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{y+z}{z}+2023\)
\(=\dfrac{y}{x}\cdot\dfrac{-z}{y}\cdot\dfrac{x}{z}+2023=2023-1=2022\)