Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Phương pháp:
Tiếp tuyến của đồ thị hàm số tại M và N song song với nhau 
Cách giải: 
Gọi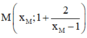 
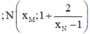là hai điểm thuộc đồ thị hàm số.
Tiếp tuyến của đồ thị hàm số tại M và N song song với nhau
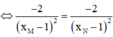
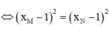
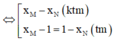
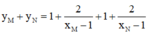
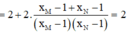
Gọi I là trung điểm của MN ta có: I(1;1)
Dễ thấy đồ thị hàm số có TCN là y = 1 và tiệm cận đứng x = 1 → I(1;1) là giao điểm của hai đường tiệm cận => C đúng.
TCN y = 1 và tiệm cận đứng x = 1 rõ ràng đi qua trung điểm I của đoạn MN=> B, D đúng
Chọn B
Cách giải: Ta có:
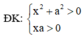
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
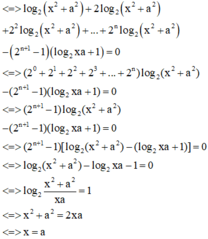
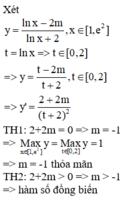
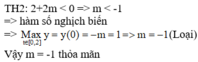
Đồ thị hàm số y = 6 - 2 x 3 x + 8 có 2 tiệm cận (đứng, ngang). Suy ra m = 2
Đồ thị hàm số y = 4 x 2 + 3 x - 1 3 x 2 + 1 có 1 tiệm cận (ngang). Suy ra n = 1
Đồ thị hàm số y = 11 4 x 2 + x - 2 có 3 tiệm cận (1ngang, 2 đứng). Suy ra p = 3
Vậy p > m > n
Đáp án C
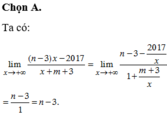
Đồ thị hàm số có tiệm cận ngang là đường thẳng
Đồ thị hàm số có tiệm cận đứng là đường thẳng
Vì đồ thị hàm số đã cho nhận trục hoành làm tiệm cận ngang và nhận trục tung làm tiệm cận đứng nên ta có:
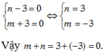
Đáp án C
* log 1 16 x xác định khi x > 0
* log 16 log 1 16 x xác định khi log 1 16 x > 0 = log 1 16 1 ⇔ 0 < x < 1
* log 1 4 log 16 log 1 16 x xác định khi
log 16 log 1 16 x > 0 = log 16 1 ⇒ log 1 16 x > 1 = log 1 16 1 16 ⇒ x < 1 16
* log 4 log 1 4 log 16 log 1 16 x xác định khi
log 1 4 log 16 log 1 16 x > 0 = log 1 4 1 ⇒ log 16 log 1 16 x < 1 = log 16 16
⇒ log 1 16 x < 16 = log 1 16 1 16 16 ⇒ x > 1 16 16
* log 1 2 log 4 log 1 4 log 16 log 1 16 x xác định khi
log 4 log 1 4 log 16 log 1 16 x > 0 = log 4 1
⇒ log 1 4 log 16 log 1 16 x > 1 = log 1 4 1 4 ⇒ log 16 log 1 16 x < 1 4 = log 16 2
⇒ log 1 16 x < 2 = log 1 16 1 16 2 ⇒ x > 1 16 2
Kết hợp tất cả các điều kiện ta được
1 16 2 < x < 1 16 ⇒ D = 1 16 2 ; 1 16 ⇒ b − a = 15 256 ⇒ m + n = 271
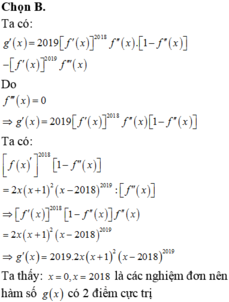
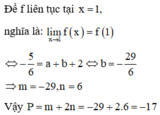
Đáp án D
Các đáp án A, B, C đều đúng, chỉ có D là sai.
Chọn phương án D.