KT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 3 2022
a, Thay x = -2 ; y = 3 ta được
\(A=\dfrac{4\left(-2\right)-5.3}{8\left(-2\right)-7.3}=\dfrac{-8-15}{-16-21}=\dfrac{23}{37}\)
b, Ta có \(\dfrac{x}{y}=\dfrac{5}{4}\Rightarrow\dfrac{x}{5}=\dfrac{y}{4}=k\Rightarrow x=5k;y=4k\)
Thay vào ta được \(A=\dfrac{4.5k-5.4k}{8.5k-7.4k}=\dfrac{0}{40k-28k}=0\)
12 tháng 2 2017
\(x-y=9\)
\(\Rightarrow x=y+9\)
Thay \(x=y+9\) vào biểu thức \(B\), ta có:
\(\frac{7x-9}{6x+y}=\frac{7\left(y+9\right)-9}{6\left(y+9\right)+y}=\frac{7y+63-9}{6y+54+y}=\frac{7y+54}{\left(6y+y\right)+54}=\frac{7y+54}{7y+54}=1\)
\(\frac{7x+9}{8x-y}=\frac{7\left(y+9\right)+9}{8\left(y+9\right)-y}=\frac{7y+63+9}{8y+72-y}=\frac{7y+72}{\left(8y-y\right)+72}=\frac{7y+72}{7y+72}=1\)
\(\Rightarrow B=\frac{7x-9}{6x+y}+\frac{7x+9}{8x-y}=1+1=2\)
Vậy \(B=2\)
12 tháng 2 2017
Thay vì cách của bạn kia, Ta có: \(x-y=9=>x=9+y\)
Thay \(x=9+y\) vào B, ta có:
\(B=\dfrac{7x-9}{6x+y}+\dfrac{7x+9}{8x-y}\)
\(=>B=\dfrac{7(y+9)-9}{6(y+9)+y}+\dfrac{7(y+9)+9}{8(y+9)-y}\)
\(=>B=\dfrac{7y+54}{7y+54}+\dfrac{7y+72}{7y+72}\)
\(=>B=1+1=2\)
B
3
24 tháng 1 2018
Với x=-1 giá trị biểu thức A là
5+2.[8.(-1)+2]=5+2.(-8+2)=5+2.(-6)=5-12= -7
Với x=-1; y=2 giá trị biểu thức B là
2.(y2-4x)=2.[22-4.(-1)]=2.(4+4)=2.8=16
CB
24 tháng 1 2018
a) Thay x vào biểu thức 5+2.(8x+2)
Ta được : 5 + 2. ( 8.(-1)+2)
= 5 + 2. (-6)
= 5 + ( -4 )
= 1
b) Thay x = -1 và y = 2 vào biểu thức 2.(\(y^2-4x\))
Ta được : \(2.\left(2^2-4.\left(-1\right)\right)\)
= 2. [ 4 - 4 . ( -1 )]
= 2. 0
= 0
YV
4
GT
8 tháng 3 2016
vì x-y=9
suy ra x=y+9
bạn thay x bằng y+9 vào biểu thức trên rồi tính ra
good lucks
TD
1
NT
0
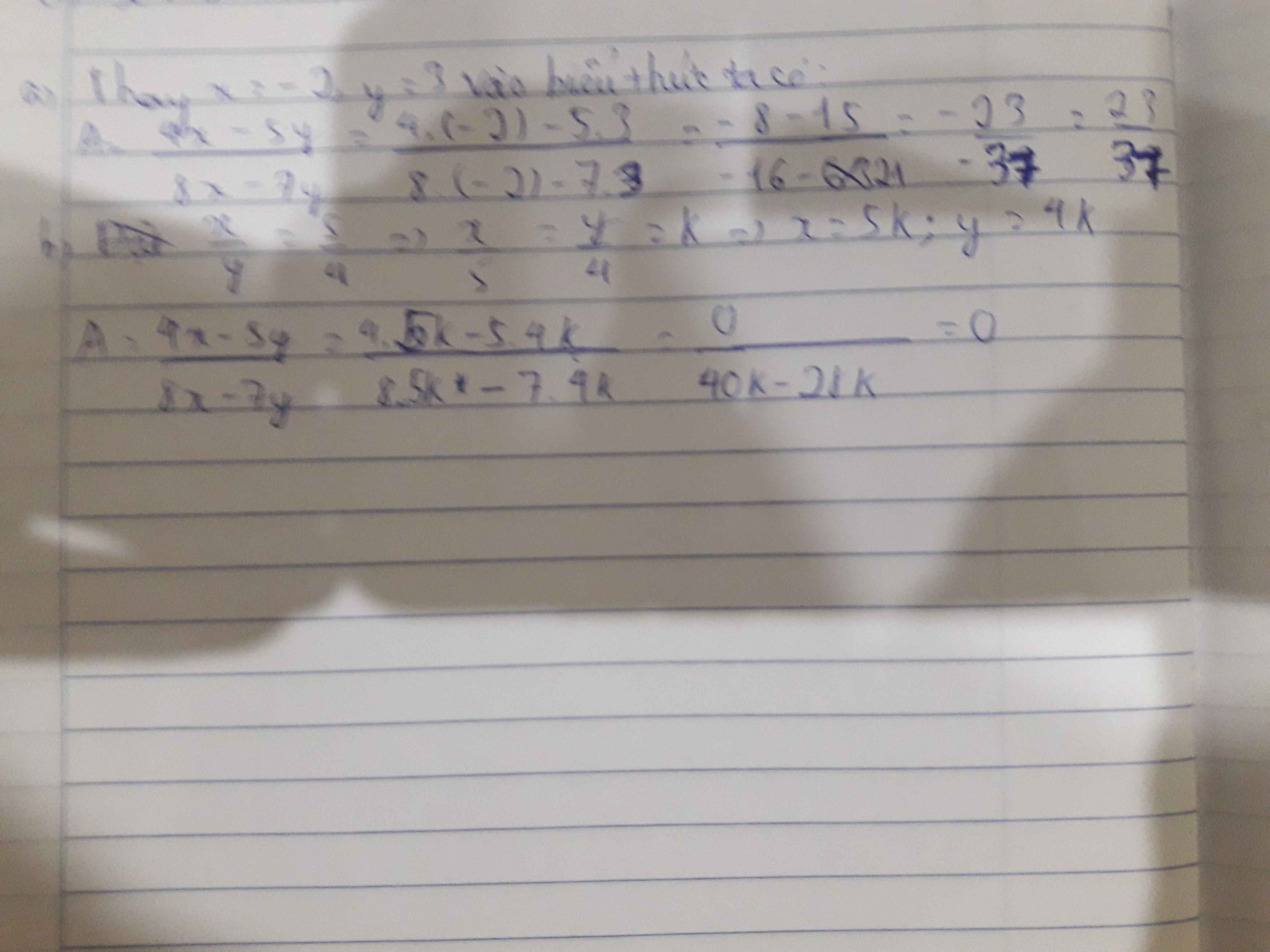
từ x-y=9=>x=y+9
thay x=y+9 vào B ta được:
\(\frac{7x-9}{6x+y}=\frac{7\left(y+9\right)-9}{6\left(y+9\right)+y}=\frac{7y+63-9}{6y+54+y}=\frac{7y+54}{\left(6y+y\right)+54}=\frac{7y+54}{7y+54}=1\) (1)
\(\frac{7x+9}{8x-y}=\frac{7\left(y+9\right)+9}{8\left(y+9\right)-y}=\frac{7y+63+9}{8y+72-y}=\frac{7y+72}{\left(8y-y\right)+72}=\frac{7y+72}{7y+72}=1\) (2)
từ (1);(2)
=>B=1-1=0
Vậy B=0