TD
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HH
0
17 tháng 9 2021
\(1,A⋮B\Leftrightarrow x^3-3x^2-ax+3=\left(x-1\right)\cdot a\left(x\right)\)
Thay \(x=1\)
\(\Leftrightarrow1-3-a+3=0\\ \Leftrightarrow a=1\)
\(2,A⋮B\Leftrightarrow3x^3-16x^2+25x+a=\left(x^2-4x+3\right)\cdot b\left(x\right)\\ \Leftrightarrow3x^3-16x^2+25x+a=\left(x-3\right)\left(x-1\right)\cdot b\left(x\right)\)
Thay \(x=1\)
\(\Leftrightarrow3-16+25+a=0\\ \Leftrightarrow a=-12\)
Thay \(x=3\)
\(\Leftrightarrow3\cdot27-16\cdot9+25\cdot3+a=0\\ \Leftrightarrow81-144+75+a=0\\ \Leftrightarrow12+a=0\Leftrightarrow a=-12\)
Vậy \(a=-12\)
29 tháng 5 2023
A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1
26 tháng 12 2021
\(=x^3\left(x+2\right)-x\left(x+2\right)\)
\(=\left(x+2\right)\cdot x\cdot\left(x+1\right)\left(x-1\right)\)
Vì đây là tích của bốn số nguyên liên tiếp
nên \(\left(x+2\right)\cdot x\cdot\left(x+1\right)\cdot\left(x-1\right)⋮24\)
CM
11 tháng 3 2019
Ta có
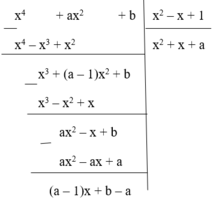
Phần dư của phép chia là R = (a – 1)x + b – A. Để phép chia trên là phép chia hết thì R = 0, Ɐx
ó (a – 1)x + b – a = 0, Ɐx
ó a - 1 = 0 b - a = 0 ó a = 1 b = 1 ó a = b
Đáp án cần chọn là: C
MT
15 tháng 10 2019
c) \(n\left(2n-3\right)-2n\left(n+1\right)\)
\(=2n^2-3n-2n^2-2n\)
\(=-5n\)Vì n nguyên
\(\Rightarrow-5n⋮5\left(đpcm\right)\)
MT
15 tháng 10 2019
a) \(\left(2n+3\right)^2-9\)
\(=\left(2n+3-3\right)\left(2n+3+3\right)\)
\(=2n\left(2n+6\right)\)
\(=4n\left(n+3\right)\)
Do \(n\in Z\Rightarrow n+3\in Z\)
\(\Rightarrow4n\left(n+3\right)⋮4\left(đpcm\right)\)
TD
5
4 tháng 11 2016
Ta có
x200 = (x200 + x198 + x196) + (- x198 - x196 - x194) + ...+ x2 = (x4 + x2 + 1)A(x) + x2
Tương tự
x100 = (x4 + x2 + 1)B(x) + x4
Từ đó ta có
x200 + x100 + 1 = (x4 + x2 + 1)A(x) + x2 + (x4 + x2 + 1)B(x) + x4 + 1
= (x4 + x2 + 1)C(x) chia hết cho x4 + x2 + 1
DT
0