
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt t = sin x − cos x = 2 sin x − π 4 .
Điều kiện − 2 ≤ t ≤ 2 .
Ta có t 2 = sin x − cos x 2 = sin 2 x + cos 2 x − 2 sin x cos x ⇒ sin 2 x = 1 − t 2 .
Phương trình đã cho trở thành 1 − t 2 + t = 1 ⇔ t 2 − t = 0 ⇔ t = 0 t = 1 .
Với t = 1, ta được 2 sin x − π 4 = 1 ⇔ sin x − π 4 = 1 2 .
Với t = 0, ta được 2 sin x − π 4 = 0 ⇔ sin x − π 4 = 0.
Chọn đáp án B.

1.
\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(1-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(1-sinx.cosx\right)\left(sinx+cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx.cosx=1\\sinx+cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=2\left(vn\right)\\\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\end{matrix}\right.\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\pi-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
2.
\(\left|cosx-sinx\right|+2sin2x=1\)
\(\Leftrightarrow\left|cosx-sinx\right|-1+2sin2x=0\)
\(\Leftrightarrow\left|cosx-sinx\right|-\left(cosx-sinx\right)^2=0\)
\(\Leftrightarrow\left|cosx-sinx\right|\left(1-\left|cosx-sinx\right|\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)=0\\\left|cosx-sinx\right|=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=k\pi\\cos^2x+sin^2x-2sinx.cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\1-sin2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\sin2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{k\pi}{2}\end{matrix}\right.\)

\(cos^3x+sin^3x=sin2x+sinx+cosx\\ \Leftrightarrow\left(sinx+cosx\right)\left(1-\dfrac{sin2x}{2}\right)=sin2x+sinx+cosx\\ \Leftrightarrow-\dfrac{1}{2}sin2x\left(sinx+cosx+2\right)=0\\ \)
Mà \(sinx+cosx=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)>-2\)
\(\Rightarrow sin2x=0\Leftrightarrow x=\dfrac{k\pi}{2}\left(k\in Z\right)\)
Tổng các nghiệm của phương trình trong \(\left[0;2018\pi\right]\) là:
\(S=\dfrac{\left(0+2018\pi\right)\left(\dfrac{2018\pi-0}{\dfrac{\pi}{2}}+1\right)}{2}=4073333\pi\)

3.
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=cos3x\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{6}\right)=sin\left(\dfrac{\pi}{2}-3x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{2}-3x+k2\pi\\x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+3x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\\x=-\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)

b:
ĐKXĐ: \(\left\{{}\begin{matrix}cosx< >0\\sinx< >0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< >\dfrac{\Omega}{2}+k\Omega\\x\ne k\Omega\end{matrix}\right.\)
=>\(x\ne\dfrac{\Omega}{2}+\dfrac{k\Omega}{2}\)
\(\dfrac{1}{cosx}+\dfrac{\sqrt{3}}{sinx}=2\cdot sin\left(x+\dfrac{\Omega}{3}\right)\)
=>\(\dfrac{sinx+\sqrt{3}\cdot cosx}{cosx\cdot sinx}=2\cdot sin\left(x+\dfrac{\Omega}{3}\right)\)
=>\(\dfrac{sinx+\sqrt{3}\cdot cosx}{cosx\cdot sinx}=2\cdot\left[sinx\cdot\cos\dfrac{\Omega}{3}+sin\left(\dfrac{\Omega}{3}\right)\cdot cosx\right]\)
=>\(\dfrac{sinx+\sqrt{3}\cdot cosx}{cosx\cdot sinx}=2\cdot\left(\dfrac{1}{2}\cdot sinx+\dfrac{\sqrt{3}}{2}\cdot cosx\right)\)
=>\(\left(sinx+\sqrt{3}\cdot cosx\right)\left(\dfrac{1}{cosx\cdot sinx}-1\right)=0\)
=>\(2\cdot\left(sinx\cdot\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\cdot cosx\right)\cdot\left(\dfrac{2}{2\cdot sinx\cdot cosx}-1\right)=0\)
=>\(2\cdot sin\left(x+\dfrac{\Omega}{3}\right)\cdot\left(\dfrac{2}{sin2x}-1\right)=0\)
=>\(\left[{}\begin{matrix}sin\left(x+\dfrac{\Omega}{3}\right)=0\\\dfrac{2}{sin2x}-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\Omega}{3}=k\Omega\\sin2x=2\left(loại\right)\end{matrix}\right.\)
=>\(x=-\dfrac{\Omega}{3}+k\Omega\)

Hướng dẫn giải
Chọn A.
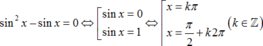
Vì 0 < x < π nên nghiệm của phương trình là x = π 2 .
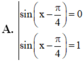
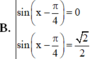
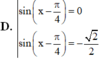
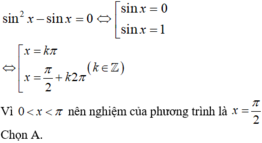
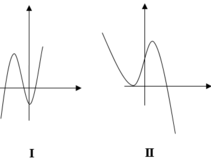
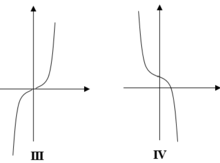

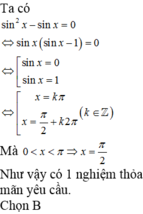
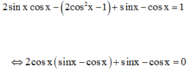
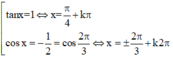
Chọn B
Bổ trợ kiến thức: Ta có thế giải bằng máy tính cầm tay CASIO fx-570VN PLUS như sau, đâu tiên dùng lệnh SHIFT SOLVE để xem 1 nghiệm bất kì có thể có của phương trình đã cho:
Đến đây ta dễ dàng chọn được phương án B là phương án đúng thay cho lời giải tự luận nhiều phức tạp.