

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




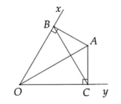
Xét ΔOBA vuông tại B và ΔOCA vuông tại C có
OA chung
\(\widehat{AOB}=\widehat{AOC}\)
Do đó: ΔOBA=ΔOCA
Suy ra: OB=OC
hay ΔOBC cân tại O
mà \(\widehat{BOC}=60^0\)
nên ΔOBC đều

a: Xét ΔOBA vuông tại B và ΔOCA vuông tại C có
OA chung
\(\widehat{AOB}=\widehat{AOC}\)
Do đó: ΔOBA=ΔOCA
Suy ra: OB=OC và AB=AC
=>ΔBOC cân tại O
b: Xét ΔABE vuông tại B và ΔACD vuông tại C có
AB=AC
\(\widehat{BAE}=\widehat{CAD}\)
Do đó:ΔABE=ΔACD
Suy ra: AE=AD

- Xét 2 tam giác vuông AOC và AOB, ta có :
+ Góc COA bằng góc BOA ( vì OA là tia phân giác của góc xOy )
+ OA là cạnh huyền chung
=> Tam giác AOC bằng AOB ( CH_GN ) => CA = CB ( 2 cạnh tương ứng ) => CAB là tam giác cân tại A
- Trong tam giác cân CAB ta có góc CAB bằng 60 độ ( Vì góc CAO bằng 180 độ trừ cho tổng hai góc AOC + OCA hay nói cách khác là góc CAO = 180 - ( 60 + 90 ) = 30
+ Mà góc CAO bằng góc BAO => góc BAO bằng 30 độ
+ Có ( góc ) CAO + BAO = CAB = 60 độ )
- Vì CAB là tam giác cân có một góc bằng 60 độ suy ra tam giác CAB là tam giác đều

Xét ΔABO vuông tại B và ΔACO vuông tại C có
OA chung
\(\widehat{BOA}=\widehat{COA}\)
Do đó: ΔABO=ΔACO
Suy ra: AB=AC
hay ΔABC cân tại A
mà \(\widehat{CAB}=180^0-120^0=60^0\)
nên ΔABC đều

Bài này mình biết làm nhưng không biết vẽ hình trên máy tính