Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\widehat{aOy}=\dfrac{\widehat{xOy}}{2}\)
\(\widehat{bOy}=\dfrac{\widehat{zOy}}{2}\)
Do đó: \(\widehat{aOy}+\widehat{bOy}=\dfrac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\dfrac{1}{2}\cdot180^0\)
hay \(\widehat{aOb}=90^0\)(đpcm)

ta có : oa là phân giác của góc xoy
ob là phân giác của góc yoz
=) góc xoa= aoy
góc yob = góc boz
=) góc boy + góc yoa = góc zob + góc xoa
(=) góc aob = góc góc zob + góc xoa
mà góc boy + góc yoa + góc góc zob + góc xoa = 180 độ
=) góc aob = góc góc zob + góc xoa = 180 độ /2 = 90 độ
=) góc aob vuông =) oa vuông góc vs ob
chúc bn học tốt

a) bOy^ + bOx^ = xOy^
Mà bOy^ = bOx^
=> 2* bOy^ = 40o
bOy^ =20o
b) bOy^ = bOx^ = 20o
=> xOa^ = bOx^ + bOa^ = 20o + 90o = 110o
Oa nằm trong góc yOz (1)
=> xOa^ + aOz^ = xOz^
aOz^ = xOz^ - xOa^ = 180o - 110o = 70o
Ta có: yOb^ + yOa^ = bOa^
yOa^ = bOa^ - yOb^ = 90o - 20o = 70o
=> aOz^ = aOy^ (2)
Từ (1) và (2) => Oa là tia phân giác của yOz^

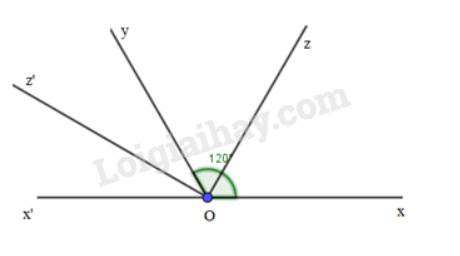
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì Oz’ là tia phân giác của \(\widehat {yOx'}\) nên \(\widehat {x'Oz'} = \widehat {yOz'} = \frac{1}{2}.\widehat {yOx'} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì tia Oy nằm trong \(\widehat {zOz'}\) nên \(\widehat {zOz'}=\widehat {zOy} + \widehat {yOz'} = 60^\circ + 30^\circ = 90^\circ \)
Vậy \(\widehat {zOy} = 60^\circ ,\widehat {yOz'} = 30^\circ ,\widehat {zOz'} = 90^\circ \)
Chú ý:
2 tia phân giác của 2 góc kề bù thì vuông góc với nhau


a. ta có \(xOy+yOz=180^0\Leftrightarrow xOy+\frac{4}{5}xOy=180^0\Rightarrow xOy=100^0\Rightarrow yOz=80^0\)
b. ta có :
\(\hept{\begin{cases}yOa=\frac{1}{2}xOy=50^0\\yOb=\frac{1}{2}yOz=40^0\end{cases}}\)
c.\(aOb=yOa+yOb=90^0\) nên Oa vuông góc với Ob

(Bạn tự vẽ hình nha)
Vì xOy và yOz là hai góc kề bù
=> Tia Oy nằm giữa ai tia Ox và Oz(1)
xOy + yOz = 180o
Vì Oa là tia phân giác của xOy
=> Tia Oa nằm giữa 2 tia Ox và Oy(2)
xOa = aOy = 1/2 xOy
Vì Ob là tia phân giác của yOz
=> Tia Ob nằm giữa hai tia Oy và Oz(3)
yOb = bOz = 1/2 yOz
Từ (1); (2) và (3) => Tia Oy nằm giữa hai tia Oa và Ob
=> aOb = aOy + yOb =\(\frac{1}{2}\widehat{xOy}+\frac{1}{2}\widehat{yOz}=\frac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\frac{1}{2}\times180^o=90^o\)
=> Oa vuông góc với Ob (đpcm)