Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

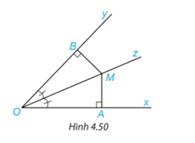
Xét hai tam giác vuông OBM và OAM có:
OM chung
\(\widehat {BOM} = \widehat {AOM}\) (gt)
\( \Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng)

Gọi E , I là giao điểm của MC với Oy;O x.
=>Tam giác EOI đều => OC = EK
Vẽ EH vuông góc MA;EK vuông góc OI dễ dàng chứng minh được
MH = MB ; EK = OC
=> MA-MB = MA – MH = HA = EK = OC
Học ~ Giỏi

Đề: Cho góc xOz = 120 độ, Oy là tia phân giác của góc xOz, Ot là tia phân giác của góc xOy. M là điểm thuộc miền trong của góc yOz. Vẽ MA vuông góc với Ox, MB vuông góc với Oy, MC vuông góc với Ot. Tính độ dài OC theo MA và MB
Gọi E , I là giao điểm của MC với Oy;O x.
=>Tam giác EOI đều => OC = EK
Vẽ EH vuông góc MA;EK vuông góc OI dễ dàng chứng minh được
MH = MB ; EK = OC
=> MA-MB = MA – MH = HA = EK = OC
Học ~ Giỏi

b: Xét ΔOMA vuông tại A và ΔOMB vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
DO đó: ΔOMA=ΔOMB
Suy ra: OA=OB
hay ΔOAB cân tại O
c: Xét ΔOEF có
ON là đường cao
ON là đường phân giác
Do đó: ΔOEF cân tại O
Suy ra: OE=OF
Xét ΔOBA có
OE/OA=OF/OB
Do đó: EF//AB