Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Bạn tự vẽ hình nha!!!
Ảnh thật, ngược chiều, và lơn hơn vật.
b)Khỏang cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{15}+\dfrac{1}{d'}\)
\(\Rightarrow d'=30cm\)
Độ cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{2}{h'}=\dfrac{15}{30}\Rightarrow h'=4cm\)

(delta) A B F O F' A' B' I
a. Tính chất: ảo thật, rõ nét, ngược chiều vật, hứng được trên màn chắn
b.Xét tam giác \(OAB\sim\) tam giác \(OA'B'\)
\(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}=\dfrac{OI}{A'B'}\) ( do OI = A'B' ) (1)
Xét tam giác \(OIF'\sim\) tam giác \(A'B'F'\)
\(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'F'}\) (2)
\(\left(1\right);\left(2\right)\Rightarrow\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}=\dfrac{OF'}{OA'-OF'}\)
\(\Leftrightarrow\dfrac{40}{OA'}=\dfrac{16}{OA'-16}\)
\(\Leftrightarrow OA'=\dfrac{80}{3}\left(cm\right)\)
Vậy khoảng cách từ ảnh đến thấu kính là \(\dfrac{80}{3}\left(cm\right)\)

Khoảng cách từ ảnh đến thấu kính là:
Áp dụng công thức tính thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=\dfrac{d.f}{d-f}=\dfrac{40.20}{40-20}=40\left(cm\right)\)
Chiều cao của ảnh là:
Ta có: \(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow h'=\dfrac{h.d'}{d}=\dfrac{20.40}{40}=20\left(cm\right)\)

Khoảng cách từ ảnh đến thấu kính:
Ta có: \(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow d'=\dfrac{h'.d}{h}=\dfrac{1,2.40}{20}=2,4\left(cm\right)\)

\(b,\) - Ảnh ảo
- Cùng chiều
- Ảnh lớn hơn vật
\(b,\) Xét \(\Delta OAB\sim\Delta OA'B'\)
\(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\left(1\right)\)
Xét \(\Delta FAB\sim\Delta FOI\)
\(\dfrac{AB}{A'B'}=\dfrac{A}{FO}\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\dfrac{OA}{OA'}=\dfrac{FA}{FO}\) mà \(FA=OF-OA\)
\(\rightarrow\dfrac{OA}{OA'}=\dfrac{OF-OA}{OF}\)
\(\rightarrow\dfrac{7}{OA'}=\dfrac{21-7}{21}\)
\(\rightarrow OA'=10,5\left(cm\right)\)

Tham khảo:
Ảnh thật, ngược chiều, lớn hơn vật và cách thấu kính một khoảng 60cm.
Lời giải: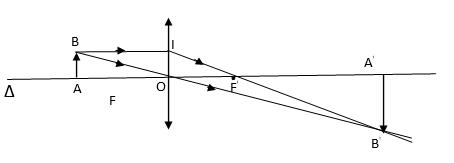
giải tính chiều cao:
ΔOAB ∼ ΔOA'B'
=> \(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\left(1\right)\)
ta lại có :
Δ OIF ∼ Δ A'B'F'
=> \(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'B'}\left(2\right)\)
Từ (1) và (2) suy ra : \(\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}\left(3\right)\)
mà : A'F' = OA' - OF ' (4)
thay số vào (3) và (4) ta được : OA' = 60cm

Ảnh ảo, ngược chiều và nhỏ hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{30}=\dfrac{1}{d'}-\dfrac{1}{20}\)
\(\Rightarrow d'=12cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{1}{h'}=\dfrac{20}{12}\Rightarrow h'=0,6cm\)