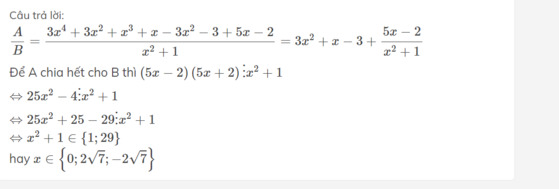Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C O D H P Q I
a. Xét tứ giác ADOH có:\(\widehat{ODA}=90^o;\widehat{DAH}=90^o;\widehat{OHA}=90^o\)
\(\Rightarrow\) ADOH là hình chữ nhật ( tứ giác có 3 góc vuông )
b. Ta có: P là điểm đối cứng của D qua O ⇒ O là trung điểm của DP(1)
Q là điểm đối xứng của H qua O ⇒ O là trung điểm của QH(2)
Ta có: \(AB\perp AC;QH\perp AC̸\) ⇒ AB//QH
Lại có: DB//QO;DB⊥DP⇒QH⊥DP(3)
Từ(1),(2),(3)⇒Tứ giác QDHP là hình thoi(Tứ giác có 2 đường chéo vuông góc và cắt nhau tại trung điểm mỗi đường)

Bài 3:
a) ta có: \(A=x^2+4x+9\)
\(=x^2+4x+4+5=\left(x+2\right)^2+5\)
Ta có: \(\left(x+2\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+2\right)^2+5\ge5\forall x\)
Dấu '=' xảy ra khi
\(\left(x+2\right)^2=0\Leftrightarrow x+2=0\Leftrightarrow x=-2\)
Vậy: GTNN của đa thức \(A=x^2+4x+9\) là 5 khi x=-2
b) Ta có: \(B=2x^2-20x+53\)
\(=2\left(x^2-10x+\frac{53}{2}\right)\)
\(=2\left(x^2-10x+25+\frac{3}{2}\right)\)
\(=2\left[\left(x-5\right)^2+\frac{3}{2}\right]\)
\(=2\left(x-5\right)^2+2\cdot\frac{3}{2}\)
\(=2\left(x-5\right)^2+3\)
Ta có: \(\left(x-5\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x-5\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x-5\right)^2+3\ge3\forall x\)
Dấu '=' xảy ra khi
\(2\left(x-5\right)^2=0\Leftrightarrow\left(x-5\right)^2=0\Leftrightarrow x-5=0\Leftrightarrow x=5\)
Vậy: GTNN của đa thức \(B=2x^2-20x+53\) là 3 khi x=5
c) Ta có : \(M=1+6x-x^2\)
\(=-x^2+6x+1\)
\(=-\left(x^2-6x-1\right)\)
\(=-\left(x^2-6x+9-10\right)\)
\(=-\left[\left(x-3\right)^2-10\right]\)
\(=-\left(x-3\right)^2+10\)
Ta có: \(\left(x-3\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x-3\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-3\right)^2+10\le10\forall x\)
Dấu '=' xảy ra khi
\(-\left(x-3\right)^2=0\Leftrightarrow\left(x-3\right)^2=0\Leftrightarrow x-3=0\Leftrightarrow x=3\)
Vậy: GTLN của đa thức \(M=1+6x-x^2\) là 10 khi x=3
Bài 2:
a) \(\left(x+y\right)^2+\left(x^2-y^2\right)\)
\(=\left(x+y\right)^2+\left(x-y\right).\left(x+y\right)\)
\(=\left(x+y\right).\left(x+y+x-y\right)\)
\(=\left(x+y\right).2x\)
c) \(x^2-2xy+y^2-z^2+2zt-t^2\)
\(=\left(x^2-2xy+y^2\right)-\left(z^2-2zt+t^2\right)\)
\(=\left(x-y\right)^2-\left(z-t\right)^2\)
\(=\left[x-y-\left(z-t\right)\right].\left(x-y+z-t\right)\)
\(=\left(x-y-z+t\right).\left(x-y+z-t\right)\)
Chúc bạn học tốt!

a, 3x - 3y = 3( x- y )
b, x2 - x =x(x - 1)
c, 3(x - y) - 5x(y - x)
= 3(x - y) + 5x(x - y)
= ( x - y)(3 + 5x)
d, x(y - 1) - y(y - 1)
= (x - y)(y - 1)
e, 10x(x - y)-8y( y - x)
= 10x(x - y) + 8y(x - y)
= (10y + 8x)(x - y)
f, 2x2 +5x3 +xy
= x(2x + 5x2 + y)
g, 14x2y - 21xy2 +28x2y2
= 7xy(2x - 3y + 4xy)
h, x2 - 3x + 2
= x2 - x - 2x + 2
= x(x - 1)- 2(x - 1)
= (x - 2)(x - 1)
i, x2 - x - 6
x2 + 2x - 3x - 6
x(x + 2) - 3(x + 2)
(x + 2)(x - 3)
k, x2 + 5x+6
= x2 - x + 6x + 6
=x(x - 1) + 6(x + 1)
= x(x - 1) - 6(x - 1)
= (x - 6)(x - 1)
l,x2 - 4x + 3
= x2 - x - 3x + 3
= x(x - 1) - 3(x - 1)
= (x - 3)(x - 1)
m, x2 + 5x +4
= x2 + x + 4x + 4
= x(x + 1) + 4(x + 1)
= (x + 4)(x + 1)

\(\dfrac{A}{B}=\dfrac{3x^4+3x^2+x^3+x-3x^2-3+5x-2}{x^2+1}=3x^2+x-3+\dfrac{5x-2}{x^2+1}\)
Để A chia hết cho B thì \(\left(5x-2\right)\left(5x+2\right)⋮x^2+1\)
\(\Leftrightarrow25x^2-4⋮x^2+1\)
\(\Leftrightarrow25x^2+25-29⋮x^2+1\)
\(\Leftrightarrow x^2+1\in\left\{1;29\right\}\)
hay \(x\in\left\{0;2\sqrt{7};-2\sqrt{7}\right\}\)

Phần a là HBA ~ ABC chứ nhỉ?
a, Xét tam giác HBA và tam giác ABC có:
góc BHA = góc BAC = 90o (ABC vg tại A và AH là đường cao)
góc B chung
\(\Rightarrow\) \(\Delta\)HBA ~ \(\Delta\)ABC (gg)
b, Vì \(\Delta\)HBA ~ \(\Delta\)ABC (cmt) (1)
Tương tự ta cx có: \(\Delta\)HAC ~ \(\Delta\)ABC (2)
Từ (1) và (2) \(\Rightarrow\) \(\Delta\)HBA ~ \(\Delta\)HAC
\(\Rightarrow\) \(\frac{AH}{CH}=\frac{BH}{AH}\) hay AH2 = CH . BH (đpcm)
Vì \(\Delta\)HBA ~ \(\Delta\)ABC (cmt)
\(\Rightarrow\) \(\frac{AB}{BC}=\frac{BH}{AB}\) hay AB2 = BC . BH (đpcm)
Vì \(\Delta\)HAC ~ \(\Delta\)ABC (cmt)
\(\Rightarrow\) \(\frac{AC}{BC}=\frac{HC}{AC}\) hay AC2 = BC . HC (đpcm)
c, Xét tam giác ABC vg tại A có: BA\(\perp\)CA
\(\Rightarrow\) BC2 = AB2 + AC2 (định lí Pytago)
BC2 = 152 + 202
BC2 = 625
BC = \(\sqrt{625}\) = 25 (cm)
Vì \(\Delta\)HBA ~ \(\Delta\)ABC (cmt)
\(\Rightarrow\) \(\frac{AB}{BC}=\frac{BH}{AB}\)
hay \(\frac{15}{25}=\frac{BH}{15}\) \(\Rightarrow\) BH = \(\frac{15^2}{25}\) = 9 (cm)
Vì BH = 9 cm nên CH = 25 - 9 = 16 (cm)
Vì \(\Delta\)HBA ~ \(\Delta\)HAC (cmt)
\(\Rightarrow\) \(\frac{AH}{CH}=\frac{BH}{AH}\) hay \(\frac{AH}{16}=\frac{9}{AH}\)
\(\Rightarrow\) \(AH^2=16\cdot9=144\)
\(\Rightarrow\) \(AH=\sqrt{144}=12\) (cm)
d, Xét tam giác ABC có: BD là tia p/g của góc ABC (gt)
\(\Rightarrow\) \(\frac{AD}{AB}=\frac{CD}{BC}\) (t/c đường p/g của tam giác)
hay \(\frac{20-CD}{15}=\frac{CD}{25}\)
\(\Leftrightarrow\) \(\frac{5\left(20-CD\right)}{75}=\frac{3CD}{75}\)
\(\Rightarrow\) 5(20 - CD) = 3CD
\(\Leftrightarrow\) 100 - 5CD = 3CD
\(\Leftrightarrow\) 3CD + 5CD = 100
\(\Leftrightarrow\) 8CD = 100
\(\Leftrightarrow\) CD = 12,5 (cm)
\(\Rightarrow\) AD = 20 - 12,5 = 7,5 (cm)
e, Ko thể có 2 điểm H được nên mk gọi D vuông góc với BC tại M nha!
Xét tam giác CMD và tam giác CAB có:
góc CMD = góc CAB = 90o (DM \(\perp\) BC và \(\Delta\)ABC vg tại A theo gt)
góc C chung
\(\Rightarrow\) \(\Delta\)CMD ~ \(\Delta\)CAB (gg)
\(\Rightarrow\) \(\frac{CM}{CA}=\frac{CD}{CB}\) hay CM . CB = CD . CA (đpcm)
Chúc bn học tốt!! (Dài quá :vvv)
a) Xét ΔHBA và ΔABC có
\(\widehat{AHB}=\widehat{CAB}\left(=90^0\right)\)
\(\widehat{ABC}\) chung
Do đó: ΔHBA∼ΔABC(g-g)(1)
Xét ΔHAC và ΔABC có
\(\widehat{AHC}=\widehat{BAC}\left(=90^0\right)\)
\(\widehat{ACB}\) chung
Do đó: ΔHAC∼ΔABC(g-g)(2)
Từ (1) và (2) suy ra ΔHBA∼ΔHAC(đpcm)
b) Ta có: ΔHBA∼ΔABC(cmt)
⇒\(\frac{HB}{AB}=\frac{BA}{BC}=\frac{HA}{AC}=k_1\)(tỉ số đồng dạng)
hay \(AB^2=BC\cdot BH\)(đpcm)
Ta có: ΔHAC∼ΔABC(cmt)
⇒\(\frac{HA}{AB}=\frac{AC}{BC}=\frac{HC}{AC}=k_2\)(tỉ số đồng dạng)
hay \(AC^2=BC\cdot HC\)(đpcm)
Ta có: ΔHBA∼ΔHAC(cmt)
⇒\(\frac{HB}{HA}=\frac{HA}{HC}=\frac{BA}{AC}=k\)(tỉ số đồng dạng)
hay \(HA^2=HB\cdot HC\)(đpcm)
c) Áp dụng định lí pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
⇔\(BC^2=15^2+20^2=625\)
hay \(BC=\sqrt{625}=25cm\)
Ta có: \(AB^2=BC\cdot BH\)(cmt)
⇔\(15^2=25\cdot BH\)
⇔\(BH=\frac{15^2}{25}=\frac{225}{25}=9cm\)
Ta có: \(\frac{HA}{AB}=\frac{AC}{BC}=\frac{HC}{AC}\)(cmt)
⇔\(\frac{HA}{15}=\frac{20}{25}\)
⇔\(HA=\frac{15\cdot20}{25}=\frac{300}{25}=12cm\)
Vậy: BC=25cm; BH=9cm; HA=12cm
d) Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\frac{AD}{AB}=\frac{CD}{CB}\)(tính chất đường phân giác của tam giác)
hay \(\frac{AD}{15}=\frac{CD}{25}\)
Ta có: AD+CD=AC(D nằm giữa A và C)
hay AD+CD=20cm
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{AD}{15}=\frac{CD}{25}=\frac{AD+CD}{15+25}=\frac{20}{40}=\frac{1}{2}\)
Do đó:
\(\left\{{}\begin{matrix}\frac{AD}{15}=\frac{1}{2}\\\frac{CD}{25}=\frac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AD=\frac{15\cdot1}{2}=7,5cm\\CD=\frac{25\cdot1}{2}=12,5cm\end{matrix}\right.\)
Vậy: AD=7,5cm; CD=12,5cm
e) Đề sai rồi bạn