Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét tam giác ADC có:
E là trung điểm AD
K là trung điểm AC
=> EK là đường trung bình
\(\Rightarrow EK=\dfrac{1}{2}CD\)
Xét tam giác ABC có:
F là trung điểm BC(gt)
K là trung điểm AC(gt)
=> KF là đường trung bình
\(\Rightarrow KF=\dfrac{1}{2}AB\)
Sửa đề: \(CM:EF\le\dfrac{AB+CD}{2}\)
Ta có: \(EF\le EK+KF=\dfrac{1}{2}AB+\dfrac{1}{2}CD=\dfrac{AB+CD}{2}\)
a: Xét ΔADC có
E là trung điểm của AD
K là trung điểm của AC
Do đó: EK là đường trung bình của ΔADC
Suy ra: EK//DC và \(EK=\dfrac{DC}{2}\)
Xét ΔABC có
K là trung điểm của AC
F là trung điểm của BC
Do đó: KF là đường trung bình của ΔABC
Suy ra: KF//AB và \(KF=\dfrac{AB}{2}\)
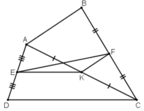
a) + ΔADC có: AE = ED (gt) và AK = KC (gt)
⇒ EK là đường trung bình của ΔADC
⇒ EK = CD/2
+ ΔABC có AK = KC (gt) và BF = FC (gt)
⇒ KF là đường trung bình của ΔABC
⇒ KF = AB/2.
b) Ta có: EF ≤ EK + KF =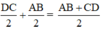 
(Bổ sung: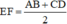 
⇔ EF = EK + KF ⇔ E, F, K thẳng hàng ⇔ AB // CD)
bài 1
a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK = CD/2
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = AB/2
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = CD/2 + AB/2= (AB +CD)/2
Vậy EF ≤ (AB +CD)/2
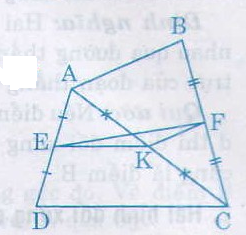
a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK = CD/2
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = AB/2
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = CD/2 + AB/2 = (AB+CD)/2
Vậy EF ≤ (AB+CD)/2
27. Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.
a) So sánh các độ dài EK và CD, KF và AB.
b) Chứng minh rằng EF \(\le\dfrac{AB+CD}{2}\)
Bài giải:
a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK =\(\dfrac{CD}{2}\)
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = \(\dfrac{AB}{2}\)
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = \(\dfrac{CD}{2}\) + \(\dfrac{AB}{2}\) = \(\dfrac{\left(AB+CD\right)}{2}\)
Vậy EF ≤ \(\dfrac{\left(AB+CD\right)}{2}\)
ta có AE=ED và AI=IC suy ra EI là đường trung bình của tam giác ADC suy ra EI=1/2 DC (1)
BF=FC và AI=IC suy ra IF là đường trung bình của tam giác ABC suy ra IF=1/2AB (2)
xét tam giác EIF có : EF<EI+IF(bất đẳng thức tam giác)
từ (1) và (2) suy ra EF<(AB+CD)/2 (3)
nếu ABCD là hình thang suy ra E,I,F thẳng hàng suy ra ÈF=(AB+CD)/2 (4)
từ (3) và (4) suy ra EF nhỏ hơn hoặc bằng (AB+CD)/2
hình tự vẽ
a) Xét tam giác ACD có:
E là trung điểm của AD (gt) ; K là trung điểm của AC (gt)
=>EK là đg trung bình của tg ACD
=>EK=1/2CD
Xét tam giác ABC có:
F là trung điểm của BC (gt);K là trung điểm của AC (gt)
=>KF là đg trung bình của tg ABC
=>KF=1/2AB
b, Xét tam giác EKF có: EF < EK + KF (bđt tam giác)
=>\(EK< \frac{1}{2}AB+\frac{1}{2}CD=\frac{1}{2}\left(AB+CD\right)\) (đpcm)
a) Xét ΔADC có
E là trung điểm của AD
K là trung điểm của AC
Do đó: EK là đường trung bình của ΔADC
Suy ra: EK//DC
Xét ΔABC có
K là trung điểm của AC
F là trung điểm của BC
Do đó: KF là đường trung bình của ΔABC
Suy ra: KF//AB
EK là đtbinh tam giác => EK=1/2 CD, KF=1/2 AB áp dụng Bđt trong tam giác EKF có EF< EK+KF =>EF< 1/2(AB+CD) . Khi K nằm giữa Evà F thì EF= EK+KF = 1/2(AB+CD) kết hợp cả 2 => đpcm