Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

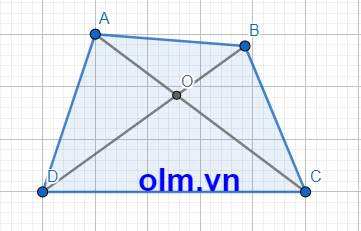
a, Xét \(\Delta\) AOB có: AO+OB > AB (trong tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Tương tự ta có: OC + OD > DC
OA + OD > AD
OB + OC > BC
Cộng vế với vế ta có:
OA+OB+OC+OD+OA+OD+OB+OC > AB +DC+AD+BC
(OA+OC)\(\times\)2 + (OB + OD)\(\times\)2 > PABCD
AC \(\times\) 2 + BD \(\times\) 2 > PABCD
AC + BD > \(\dfrac{P_{ABCD}}{2}\) (đpcm)
b, Xét \(\Delta\) ABD có: AB + AD > BD (trong tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại)
Tương tự ta có: AD + DC > AC
DC + CB > DB
CB + AB > AC
Cộng vế với vế ta có:
AB+AD+AD+DC+DC+CB+CB+AB >BD+ AC+DB+AC
2AB+2BC+2CD+2AD> 2AC + 2BD
2(AB + BC + CD + AD) > 2(AC + BD)
AB + BC + CD + AD > AC + BD
PABCD > AC + BD (đpcm)

Hi vọng bạn có kiến thức vững về BĐT tam giác nha, mấy bài này toàn BĐT tam giác thoi, mình ko chứng minh lại đâu.
Bài 3:
a) Xét tam giác AOB: \(OB>AB-AO\)
Xét tam giác DOC: \(OD>DC-OC\)
Cộng vế theo vế: \(OB+OD>AB+DC-\left(AO+OC\right)\Leftrightarrow BD>AB+DC-AC\Leftrightarrow BD+AC>AB+DC\)
b) Hoàn toàn tương tự với 2 tam giác AOD và BOC:
\(\Rightarrow\hept{\begin{cases}OD>AD-AO\\OB>BC-OC\end{cases}\Rightarrow BD>AD+BC-AC\Leftrightarrow BD+AC>AD+BC}\)
Bài 4:
a) Từ câu 3 ta có \(\hept{\begin{cases}BD+AC>AB+CD\\BD+AC>AD+BC\end{cases}}\)Cộng vế theo vế:
\(\Rightarrow2\left(BD+AC\right)>AB+BC+CD+DA=P_{ABCD}\Rightarrow BD+AC>\frac{P_{ABCD}}{2}\)
b) Câu này thực ra không cần đề cho trước \(AC< \frac{P_{ABCD}}{2}\)đâu, vì đây là điều hiển nhiên mà
Xét 2 tam giác ABC và ADC: \(\hept{\begin{cases}AC< AB+BC\\AC< AD+DC\end{cases}}\)cộng vế theo vế:
\(\Rightarrow2AC< AB+BC+CD+DA=P_{ABCD}\Rightarrow AC< \frac{P_{ABCD}}{2}\)(1)
Hoàn toàn tương tự với 2 tam giác ABD và CBD \(\Rightarrow BD< \frac{P_{ABCD}}{2}\)(2)
Cộng (1) và (2) vế theo vế: \(AC+BD< P_{ABCD}\)


Xét tứ giác ABCD có
AC cắt BD tại trung điểm của mỗi đường
góc BAD=90 độ
=>ABCD là hình chữ nhật

cho tứ giác ABCD. Gọi M,N,P,Q lần lượt là tđ của AB,BC,CD,DA.
a) tứ giác MNPQ là hình gì ? vì sao?
MN//BD; PQ//BD
NP//AC; QM//AC
=>MN//PQNP//QNMNPQ la hbbh


Tứ giác ABCD là một hình vuông.