Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1)
a) Vì A: B:C:D = 1:2:3:4
=> A= B/2 = C/3=D/4
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
A = 36 độ
B= 72 độ
C=108 độ
D= 144 độ
b) Ta có :
A + D = 36 + 144 = 180 độ(1)
B+C = 72 + 108 = 180 độ(2)
Từ (1) và (2) ta có:
=> AB //CD (dpcm)
c) Ta có :
CDE + ADC = 180 độ(kề bù)
=> CDE = 180 - 144 = 36
Ta có :
BCD + DCE = 180 độ ( kề bù)
=> DCE = 180 - 108 = 72
Xét ∆CDE ta có :
CDE + DCE + DEC = 180 ( tổng 3 góc trong ∆)
=> DEC = 180 - 72 - 36 = 72 độ
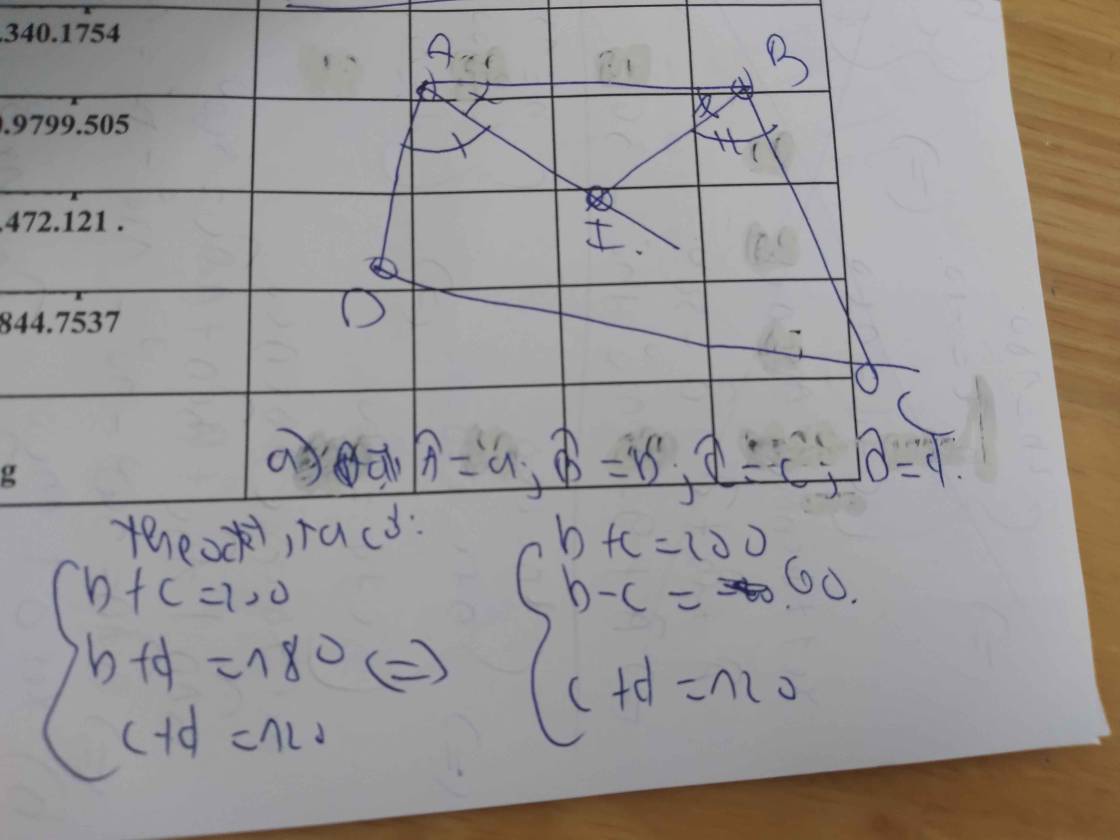
Bài 2)
a) Ta có ABCD có :
A + B + C + D = 360 độ
Mà C = 80 độ
D= 70 độ
=> A+ B = 360 - 80 - 70 = 210 độ
Ta có AI là pg góc A
BI là pg góc B
=> DAI = BAI = A/2
=> ABI = CBI = B/2
=> BAI + ABI = A + B /2
=> BAI + ABI = 210/2 = 105
Xét ∆IAB ta có :
IAB + ABI + AIB = 180 độ
=> AIB = 180 - 105
=> AIB = 75 độ
=>

Bài 1)
Trên AD lấy E sao cho AE = AB
Xét ∆ACE và ∆ACB ta có :
AC chung
DAC = BAC ( AC là phân giác)
AB = AE (gt)
=> ∆ACE = ∆ACB (c.g.c)
=> CE = CB (1)
=> AEC = ABC = 110°
Mà AEC là góc ngoài trong ∆EDC
=> AEC = EDC + ECD ( Góc ngoài ∆ bằng tổng 2 góc trong không kề với nó)
=> ECD = 110 - 70
=> EDC = 40°
Xét ∆ EDC :
DEC + EDC + ECD = 180 °
=> CED = 180 - 70 - 40
=> CED = 70°
=> CED = EDC = 70°
=> ∆EDC cân tại C
=> CE = CD (2)
Từ (1) và (2) :
=> CB = CD (dpcm)
b) Ta có thể thay sao cho tổng 2 góc đối trong hình thang phải = 180°

a: Xét ΔMNQ có
A là trung điểm của MN
B là trung điểm của MQ
Do đó: AB là đường trung bình của ΔMNQ
Suy ra: AB//NQ và AB=NQ/2(1)
Xét ΔNPQ có
C là trung điểm của QP
D là trung điểm của NP
Do đó: CD là đường trung bình của ΔNPQ
Suy ra: CD//NQ và CD=NQ/2(2)
Từ (1) và (2) suy ra ABCD là hình bình hành

a: ABCD là hình bình hành
=>\(\widehat{BAD}+\widehat{ABC}=180^0;\widehat{ABC}+\widehat{BCD}=180^0;\widehat{ADC}+\widehat{BCD}=180^0;\widehat{BAD}+\widehat{ADC}=180^0\)
\(\widehat{BAD}+\widehat{ABC}=180^0\)
=>\(2\cdot\left(\widehat{MAB}+\widehat{MBA}\right)=180^0\)
=>\(\widehat{MAB}+\widehat{MBA}=90^0\)
=>\(\widehat{AMB}=90^0\)
=>AM vuông góc MB
=>AN vuông góc BQ
b: \(\widehat{ADC}+\widehat{BCD}=180^0\)
=>\(2\cdot\left(\widehat{PDC}+\widehat{PCD}\right)=180^0\)
=>\(\widehat{PDC}+\widehat{PCD}=90^0\)
=>ΔPCD vuông tại P
=>\(\widehat{CPD}=90^0\)
=>\(\widehat{NPQ}=90^0\)
\(\widehat{BAD}+\widehat{ADC}=180^0\)
=>\(2\cdot\left(\widehat{NAD}+\widehat{NDA}\right)=180^0\)
=>\(\widehat{NAD}+\widehat{NDA}=90^0\)
=>ΔNAD vuông tại N
=>\(\widehat{AND}=90^0\)
=>\(\widehat{MNP}=90^0\)
Xét tứ giác MNPQ có
\(\widehat{MNP}=\widehat{NMQ}=\widehat{NPQ}=90^0\)
=>MNPQ là hình chữ nhật


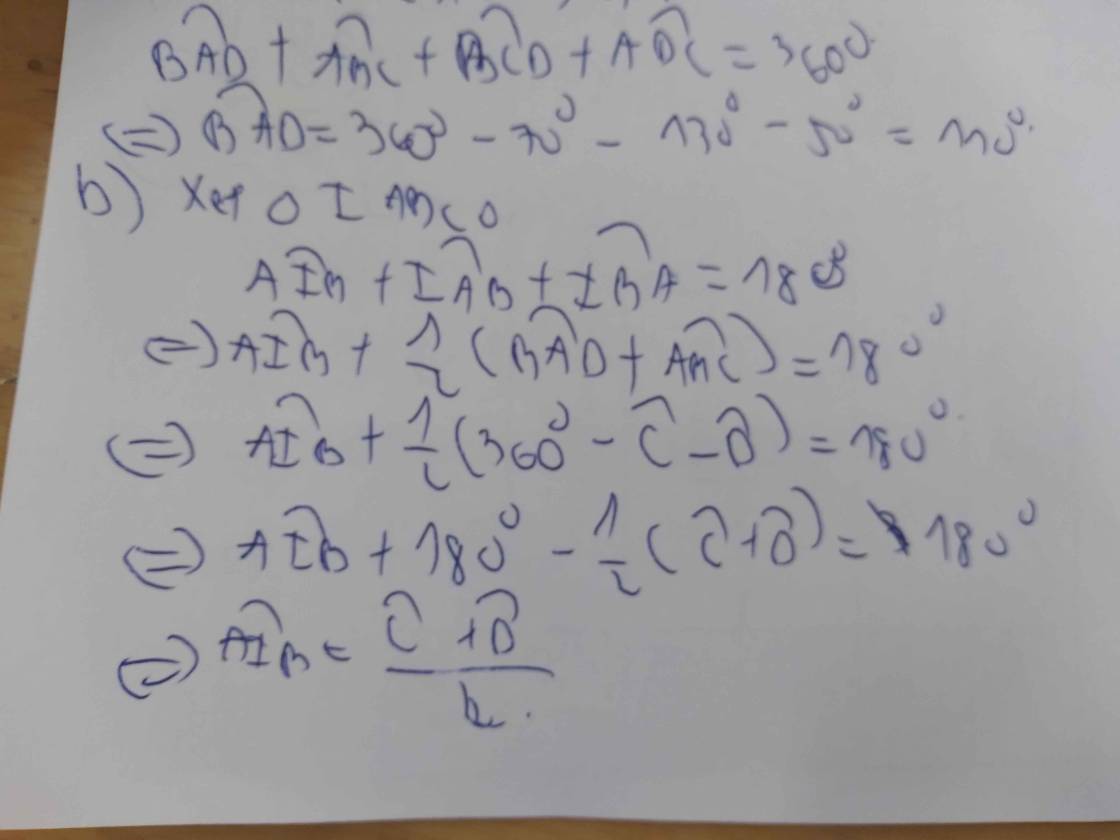
Đáp án C