Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Vì ABCD là hình bình hành
=> OA=OC, OB=OD
Ta có: OM=OA/2
OP=OC/2
Mà OA=OC => OM=OP
Cm tương tự ta được OQ=ON
Tứ giác MNPQ có OM=OP. OQ=ON
=> MNPQ là hình bình hành
2) Tứ giác ANCQ có OA=OC (cmt), OQ=ON (cmt)
Suy ra tứ giác ANCQ là hình bình hành
Tứ giác BPDM có OB=OD (cmt), OM=OP (cmt)
Suy ra tứ giác BPDM là hình bình hành
Hai đoạn thẳng AB và CD cắt nhau tại 0. Biết rằng OA = OC, OB = OD. Tứ giác ABCD là hình gì ? Vì sao

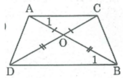
Ta có: OA = OC (gt)
⇒ ∆ OAC cân tại O
⇒ ∠ A 1 = ( 180 0 - ∠ (AOC) ) / 2 (tính chất tam giác cân) (1)
OB = OD (gt)
⇒ ∆ OBD cân tại O
⇒ ∠ B 1 = ( 180 0 - ∠ (BOD) )/2 (tính chất tam giác cân) (2)
∠ (AOC) = ∠ (BOD) (đối đỉnh) (3)
Từ (1), (2), (3) suy ra: ∠ A 1 = ∠ B 1
⇒ AC // BD (vì có cặp góc ở vị tri so le trong bằng nhau)
Suy ra: Tứ giác ACBD là hình thang
Ta có: AB = OA + OB
CD = OC + OD
Mà OA = OC, OB = OD
Suy ra: AB = CD
Vậy hình thang ABCD là hình thang cân.

Ta có: OA = OC (gt)
⇒ ∆ OAC cân tại O
⇒ˆA1=1800–ˆAOC2⇒A^1=1800–AOC^2 (tính chất tam giác cân) (1)
OB = OD (gt)
⇒ ∆ OBD cân tại O
⇒ˆB1=1800–ˆBOD2⇒B^1=1800–BOD^2 (tính chất tam giác cân) (2)
ˆAOC=ˆBODAOC^=BOD^ (đối đỉnh) (3)
Từ (1), (2) và (3) suy ra: ˆA1=ˆB1A^1=B^1
⇒ AC // BD (vì có cặp góc ở vị trí so le trong bằng nhau)
Suy ra: Tứ giác ACBD là hình thang
Ta có: AB = OA + OB
CD = OC + OD
Mà OA = OC, OB = OD
Suy ra: AB = CD
Vậy hình thang ACBD là hình thang cân.

giả dụ ta có hình thang cân ABCD
góc D=50o mà góc D= góc C
=> góc C= 500
Mà góc D + góc A=180o
=> góc A =180o-50o=130o
chứng minh tương tự ta cũng có góc B=1300
Ta có : OA=OC;OB=OD
Theo dấu hiệu nhận biết số 5 thì tứ giác có 2 đường chéo cắt nhau tại tđ của mỗi đường là hình bình hành.
VẬy tứ giác ABCD là hình bình hành
ABCD là hình bình hành