Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó; AHMK là hình chữ nhật

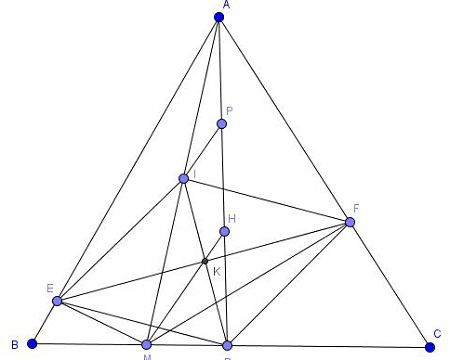 Các tam giác vuông AEM và ADM có EI và DI là trung tuyến ứng với AM nên
Các tam giác vuông AEM và ADM có EI và DI là trung tuyến ứng với AM nên
=> EI = DI ( = ½ AM)
=> Tam giác EID cân tại I
Lại có các tam giác AEI và ADI cân tại I nên:
^EIM = 2^EAI và ^MID = 2^IAD
=> ^EID = ^EIM + ^MID = 2(^EAI + ^IAD) = 2^EAD = 2. 30 = 60 độ
(Vì AD là đường cao nên là phan giác ^A)
Tam giác EID cân lại có ^EID = 60 độ nên đều
Tương tự tam giác IFD đều nên: EI = IF = FD = DE => Tứ giác DEIF là hình thoi
b) Gọi O là giao EF và DI và K là trung điểm AH, ta có IK là trng bình tam giác AMH và OH là trung bình tam giác AID.
=> HO//IK và HM//IK
=> Tia HO và HM trùng nhau hay M, H, O thẳng hàng => MH, ID, EF đồng quy tại O

dạ cô vẽ dùng em hình
a, xét tứ giác AHMK có
góc MHA=90 độ( MH ⊥ Ab-gt)
góc MKA=90 độ( MK⊥ AC-gt)
góc HAK= 90 độ ( tam giác ABC vuông tại A-gt)
-> AHMK là hcn ( tứ giác có 3 góc vuông là hcn)2). Có : MH vuông góc với AB ( gt )
AC vuông góc với AB (
Δ
ABC vuông tại A)
=> MH//AC
Xét tam giác ABc có
MH//AC( cmt)
M là trung điểm BC (gt)
=> H là trung điểm AB (định lý đường trung bình của tam giác)(đpcm)
. Có: MK vuông góc AC ( gt)
AB vuông góc AC( tam giác ABC vuông tại A )
=> MK//AB
Có:MK//AB(cmt)
M là trung điểm BC ( gt)
=> K là trung điểm AC ( định lý đường trung bình của tam giác )
Có : H là trung điểm AB ( cmt)
=. BH=1/2AB
Xét tam giác ABC có
M là trung điểm BC(cmt)
K là trung điểm AC ( cmt)
=> MK là đưởng trung bình của tam giác ABC( dấu hiệu nhận biết)
=> MK=1/2AB
( tính chất đường trung bình của tam giác)
=> MK//AB(tính chất đường trung bình của tam giác) hay MK//BH
Có MK=1/2AB
BH= 1/2AB
=> MK=BH
Mà MK//BH(cmt)
=> BMKH là hình bình hành
VÌ BMKH là hình bình hành (cmt)
=> Hai đường chéo HM và BK cắt nhau tại trung điểm mỗi đường
Mà E là trung điểm HM ( gt)
=> E là trung điểm BK hay ba điểm B; E; K thẳng hàng(dpcm)
mình tự làm ne chắc do mạng mình bị lỗi bắm nhầm phải
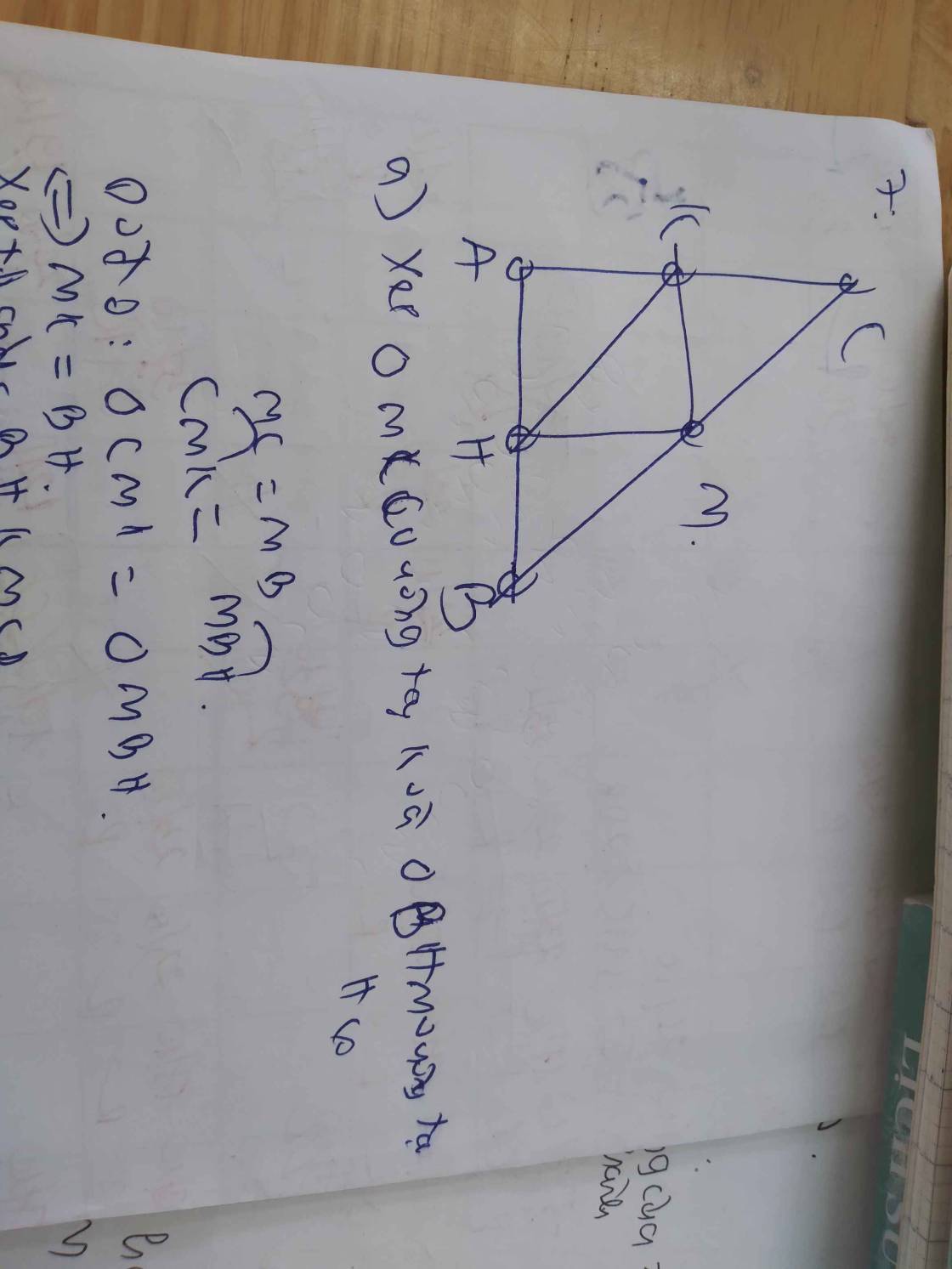



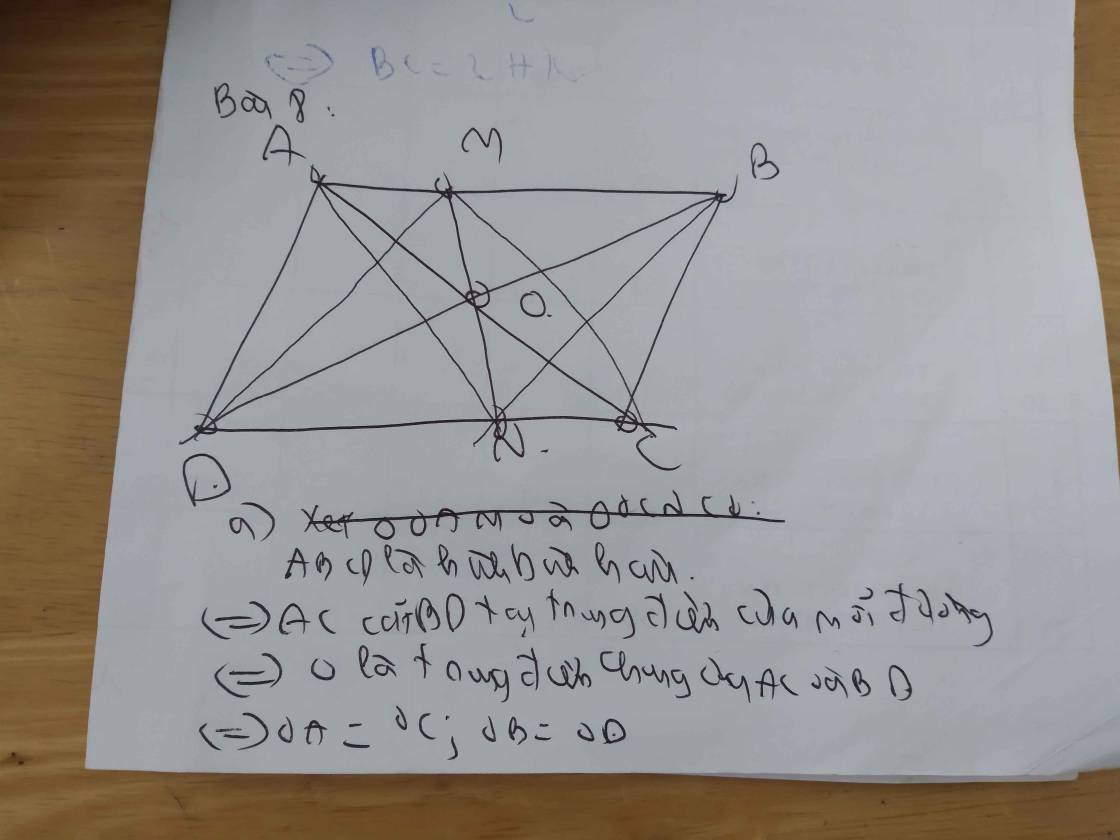

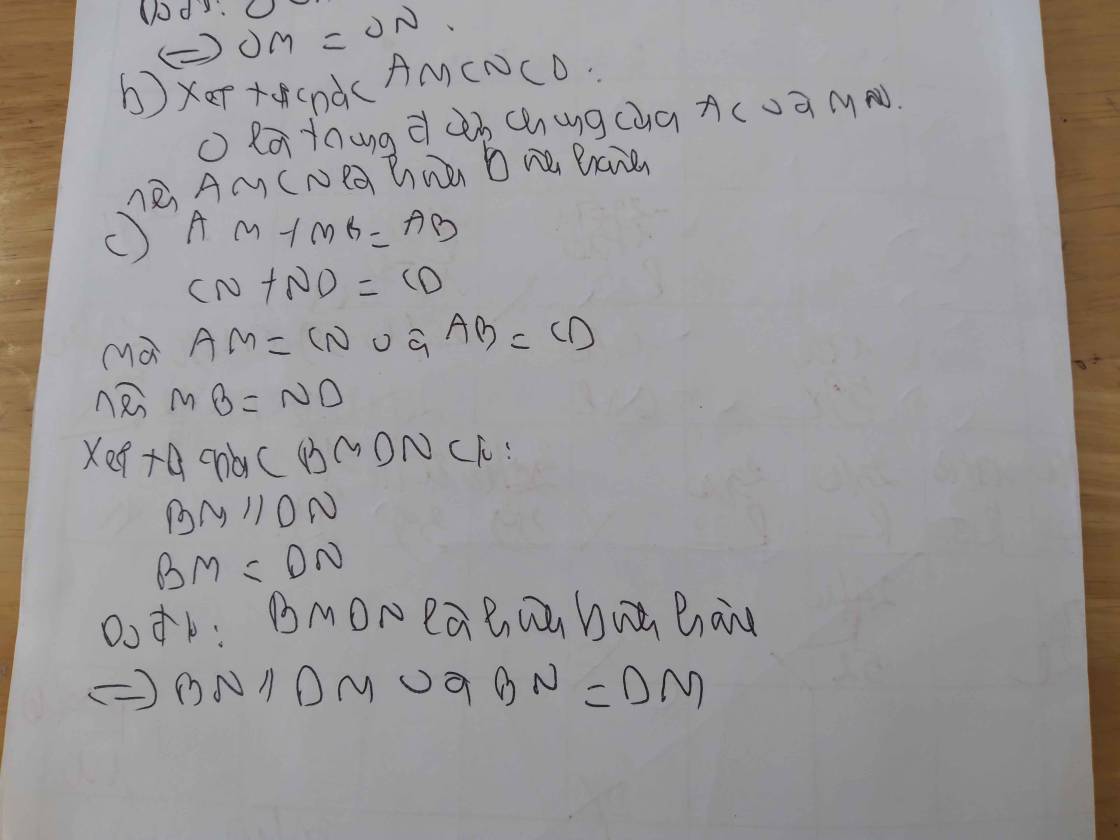
a) Ta có: MK⊥AD(gt)
CD⊥AD(gt)
Do đó: MK//CD(Định lí 1 từ vuông góc tới song song)
Xét ΔAKM và ΔADC có
\(\widehat{MAK}\) chung
\(\widehat{AMK}=\widehat{ACD}\)(hai góc so le trong, MK//CD)
Do đó: ΔAKM∼ΔADC(g-g)